Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

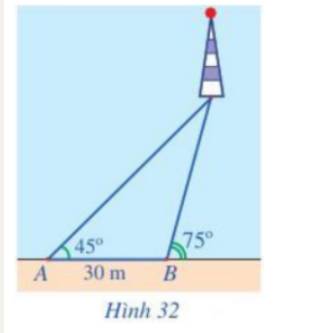
Gọi C là vị trí ngọn hải đăng và H là hình chiếu của C trên AB.
Khi đó CH là khoảng cách từ ngọn hải đăng tới bờ biển.
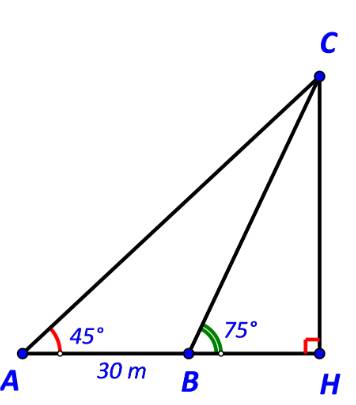
Ta có: \( \widehat {ACB} = \widehat {HBC} - \widehat {BAC} = {75^o} - {45^o} = {30^o}; \, \widehat {ABC} = {180^o} - {75^o} = {105^o}\)
Áp dụng định lí sin trong tam giác ABC ta có:
\(\frac{{AB}}{{\sin C}} = \frac{{AC}}{{\sin B}}\)
\( \Rightarrow AC = \sin B.\frac{{AB}}{{\sin C}} = \sin {105^o}.\frac{{30}}{{\sin {{30}^o}}} \approx 58\)
Tam giác ACH vuông tại H nên ta có:
\(CH = \sin A.AC = \sin {45^o}.58 \approx 41\)
Vậy ngọn hải đăng cách bờ biển 41 m.

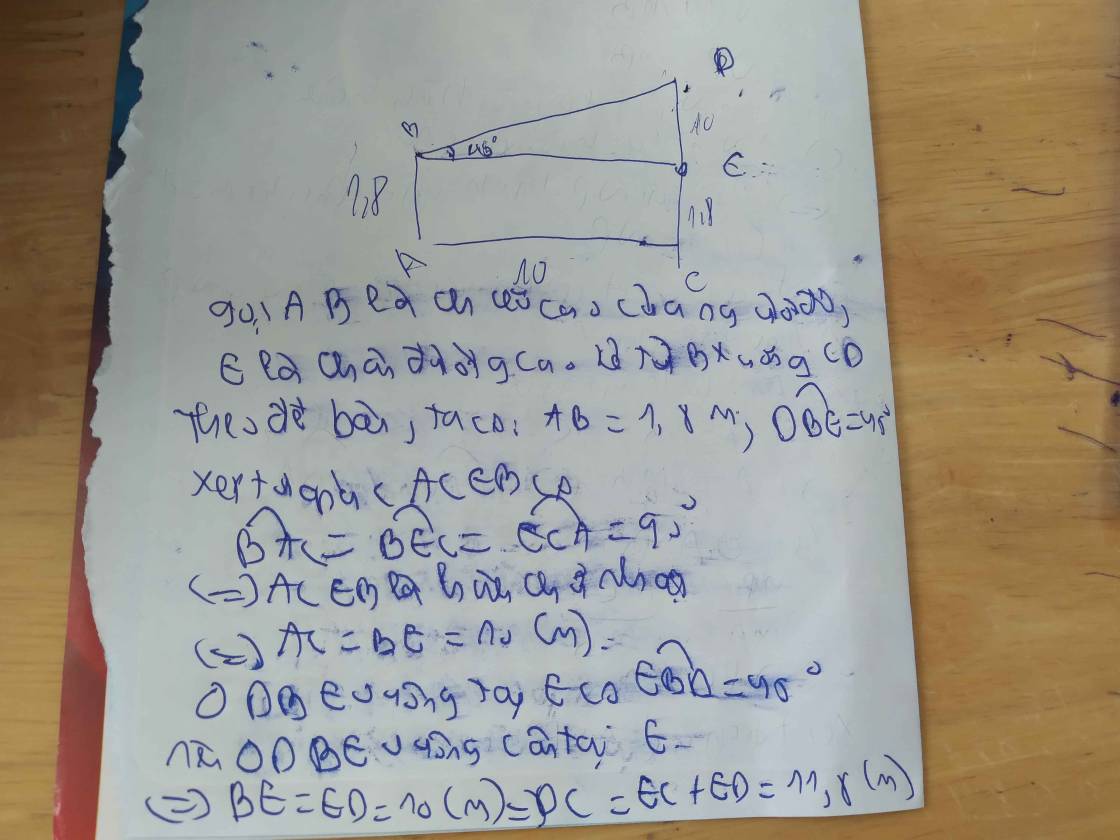
\(tan45^o=\dfrac{CD-1,8}{10}\) (CD là chiều cao cây bàng)
\(\Rightarrow CD-1,8=10.tan45^o\)
\(\Rightarrow CD=10.1+1,8=11,8\left(m\right)\)

Tam giác \(AHB\) vuông tại $H$ nên $AB^2=AH^2+HB^2=4^2+20^2=416$
\(\Rightarrow AB \approx 20,4\)
\(tan\widehat {BAH} = \frac{{HB}}{{HA}} = \frac{{20}}{4} = 5\\
\Rightarrow {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \widehat {BAH} \approx {78,7^0}\\
\Rightarrow {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \widehat {HAC} \approx {78,7^0} + {45^0} \approx {123,7^0}
\)
\( {\widehat {HAB} + \widehat {HBA} = {{90}^0}}\\ {\widehat {ABC} + \widehat {HBA} = {{90}^0}}\\ { \Rightarrow \widehat {HAB} = \widehat {ABC}}\\ { \Rightarrow \widehat {BCA} = {{180}^0}-\widehat {BAC}-\widehat {ABC} = {{180}^0}-\widehat {HAC}} \)
\( \Rightarrow {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \widehat {BCA} \approx {180^0}-{123,7^0} = {56,3^0}.\)
Ta có: \(\frac{{BC}}{{{\rm{sin}}{{45}^0}}} = \frac{{AB}}{{{\rm{sin}}{{56,3}^0}}}\)
\(\Rightarrow {\mkern 1mu} {\mkern 1mu} BC = \frac{{20,4}}{{{\rm{sin}}{{56,3}^0}}}{\rm{sin}}{45^0} \approx 17,4\)
Vậy \(BC\approx17,4m\)
Tam giác \(AHB\) vuông tại H nên \(A{B^2} = A{H^2} + H{B^2} = {4^2} + {20^2} = 416\)
\(\Rightarrow AB \approx 20,4\)
\(tan\widehat {BAH} = \frac{{HB}}{{HA}} = \frac{{20}}{4} = 5\\
\Rightarrow {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \widehat {BAH} \approx {78,7^0}\\
\Rightarrow {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \widehat {HAC} \approx {78,7^0} + {45^0} \approx {123,7^0}
\)
\( {\widehat {HAB} + \widehat {HBA} = {{90}^0}}\\ {\widehat {ABC} + \widehat {HBA} = {{90}^0}}\\ { \Rightarrow \widehat {HAB} = \widehat {ABC}}\\ { \Rightarrow \widehat {BCA} = {{180}^0}-\widehat {BAC}-\widehat {ABC} = {{180}^0}-\widehat {HAC}} \)
\( \Rightarrow {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \widehat {BCA} \approx {180^0}-{123,7^0} = {56,3^0}.\)
Ta có: \(\frac{{BC}}{{{\rm{sin}}{{45}^0}}} = \frac{{AB}}{{{\rm{sin}}{{56,3}^0}}}\)
\(\Rightarrow {\mkern 1mu} {\mkern 1mu} BC = \frac{{20,4}}{{{\rm{sin}}{{56,3}^0}}}{\rm{sin}}{45^0} \approx 17,4\)
Vậy \(BC\approx17,4m\)

ve hinh thang vuong ABED co AD//BC ; va ED vuong goc voi BC keo dai ;
E thuoc BC keo dai(hinh chieu cua BC tren mat dat)
.D la diem duoi mat dat cua A AD=7m; BC=5m
Cac goc 40 ; 50 do la giua AC ; AB voi phuong nam ngang .
Ta tinh duoc DE theo BC : DE =BC/(tan50-tan40)
=> Bc da biet tan ta tra duoc .Con CE la chieu cao cua nha :
Vay : CE=AD+DE*tan40= 7+5*tan40/(tan50-tan40)

Tham khảo:
a)
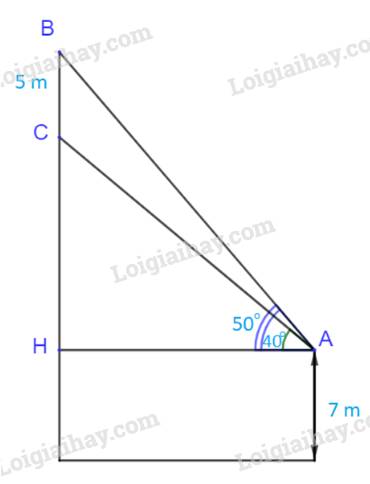
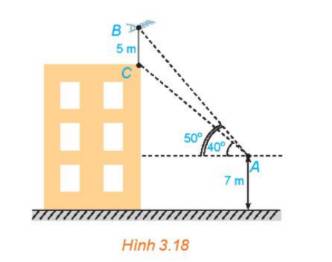
Gọi H là hình chiếu của A lên đường thẳng BC.
Ta có: \(\widehat {HAB} = {50^o}\); \(\widehat {HAC} = {40^o}\)
\( \Rightarrow \widehat {BAC} = {50^o} - {40^o} = {10^o}\) (1)
Xét tam giác ABH, vuông tại H ta có:
\(\widehat H = {90^o};\;\widehat {BAH} = {50^o}.\)
\( \Rightarrow \widehat {HBA} = {180^o} - {90^o} - {50^o} = {40^o}\) hay \(\widehat {CBA} = {40^o}\). (2)
Từ (1) và (2), suy ra: \(\widehat {BCA} = {180^o} - {40^o} - {10^o} = {130^o}.\)
Vậy ba góc của tam giác ABC lần lượt là: \(\widehat A = {10^o};\;\widehat B = {40^o};\;\widehat C = {130^o}\).
b)
Áp dụng định lý sin cho tam giác ABC, ta được:
\(\frac{{BC}}{{\sin A}} = \frac{{AC}}{{\sin B}} = \frac{{AB}}{{\sin C}}\) \( \Rightarrow AB = \frac{{BC.\sin C}}{{\sin A}}\)
Mà: \(BC = 5\;(m);\;\;\widehat C = {130^o};\;\widehat A = {10^o}\)
\( \Rightarrow AB = \frac{{5.\sin {{130}^o}}}{{\sin {{10}^o}}} \approx 22\;(m)\)
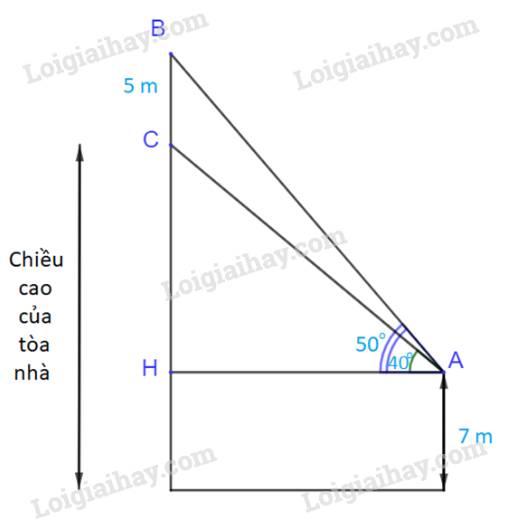
Xét tam giác ABH, vuông tại H ta có:
\(\sin \widehat {BAH} = \frac{{BH}}{{AB}}\)\( \Rightarrow BH = AB.\,\,\sin \widehat {BAH}\)
Mà: \(AB \approx 22\;(m);\;\;\widehat {BAH} = {50^o}\)
\( \Rightarrow BH \approx 22.\sin {50^o} \approx 16,85\;(m)\)
Vậy chiều cao của tòa nhà là: \(BH-{\rm{ }}BC + 7 = 16,85-5 + 7 = 18,85{\rm{ }}\left( m \right)\)

Gọi A là vị trí đứng của Nam, B là điểm cao nhất của cây, C là vị trí gốc cây.
Gọi H là hình chiếu của A trên BC. Ta có hình vẽ:
TH1: Cây cao hơn tòa nhà

Ta có: \(\tan {24^ \circ } = \frac{{BH}}{{AH}} \Rightarrow BH = 30.\tan {24^ \circ } \approx 13,357\)
\( \Rightarrow BC = BH + HC \approx 13,357 + 1,5 + 18,5 = 33,357(m)\)
TH2: Cây thấp hơn tòa nhà
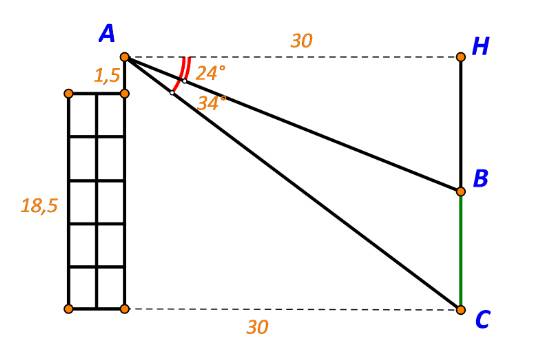
Ta có: \(\tan {24^ \circ } = \frac{{BH}}{{AH}} \Rightarrow BH = 30.\tan {24^ \circ } \approx 13,357\)
\( \Rightarrow BC = HC -HB \approx 1,5 + 18,5 - 13,357= 6,643(m)\)