Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 1:
a: Vì I thuộc trục Ox nên I(x;0)
\(\overrightarrow{AI}=\left(x+1;-1\right)\)
\(\overrightarrow{AB}=\left(1;2\right)\)
Vì A,I,B thẳng hàng nên \(\dfrac{x+1}{1}=-\dfrac{1}{2}\)
=>x=-3/2
b: \(\overrightarrow{AM}=\left(m+5;2m\right)\)
Vì A,M,B thẳng hàng nên \(\dfrac{m+5}{1}=\dfrac{2m}{2}\)
=>m+5=m(vô lý)

A(m-1;-1); B(2;2-2m); C(m+3;3)
\(\overrightarrow{AB}=\left(2-m+1;2-2m+1\right)\)
=>\(\overrightarrow{AB}=\left(3-m;3-2m\right)\)
\(\overrightarrow{AC}=\left(m+3-m+1;3+1\right)\)
=>\(\overrightarrow{AC}=\left(4;4\right)\)
Để A,B,C thẳng hàng thì \(\dfrac{3-m}{4}=\dfrac{3-2m}{4}\)
=>3-m=3-2m
=>m=0
\(\left\{{}\begin{matrix}\overrightarrow{AB}=\left(3-m;3-2m\right)\\\overrightarrow{AC}=\left(4;4\right)\end{matrix}\right.\)
3 điểm A;B;C thẳng hàng khi và chỉ khi \(\overrightarrow{AB}=k\overrightarrow{AC}\) với \(k\ne0\)
Hay \(\dfrac{3-m}{4}=\dfrac{3-2m}{4}\Rightarrow m=0\)

Gọi \(M\left(0;m\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AM}=\left(-1;m+2\right)\\\overrightarrow{AB}=\left(-5;7\right)\end{matrix}\right.\)
3 điểm M;A;B thẳng hàng khi:
\(\dfrac{-1}{-5}=\dfrac{m+2}{7}\Rightarrow m=-\dfrac{3}{5}\)
\(\Rightarrow M\left(0;-\dfrac{3}{5}\right)\)


Lời giải:
Gọi tọa độ điểm \(M=(0,a)\)
Khi đó vecto biểu diễn đoạn thẳng \(MA,MB\) lần lượt là:
\(\overrightarrow{MA}=(-1,1-a)\) và \(\overrightarrow {MB}=(3,2-a)\)
Ta có \(\cos \angle AMB=\cos (\overrightarrow{MA},\overrightarrow{MB})=\frac{|(-1).3+(1-a)(2-a)|}{\sqrt{1+(a-1)^2}.\sqrt{3^2+(a-2)^2}}\)
\( \Leftrightarrow \frac{|(a-1)(a-2)-3|}{\sqrt{1+(a-1)^2}\sqrt{9+(a-2)^2}}=\cos 45=\frac{\sqrt{2}}{2}\)
\(\Leftrightarrow (a+3)(a-2)(a^2-7a+4)=0\)
\(\Rightarrow\left[{}\begin{matrix}a=-3\\a=2\\a=\dfrac{7\pm\sqrt{33}}{2}\end{matrix}\right.\)

\(\left\{{}\begin{matrix}x=2+t\\y=1-3t\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}3x=6+3t\\y=1-3t\end{matrix}\right.\) \(\Rightarrow3x+y=7\Rightarrow3x+y-7=0\)
Vậy (d) có pt tổng quát là: \(3x+y-7=0\)
A và B nằm cùng phía đối với d khi và chỉ khi:
\(\left(3.1+2-7\right)\left(3.\left(-2\right)+m-7\right)>0\)
\(\Leftrightarrow-2\left(m-13\right)>0\)
\(\Rightarrow m< 13\)

\(\overrightarrow{AB}=\left(-6;-3\right)=-3\left(2;1\right)\Rightarrow\) đường thẳng AB nhận \(\left(2;1\right)\) là 1 vtcp
Phương trình tham số đường thẳng AB có dạng: \(\left\{{}\begin{matrix}x=5+2t\\y=4+t\end{matrix}\right.\)
Do M thuộc AB nên tọa độ M có dạng \(M\left(5+2t;4+t\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{MA}=\left(-2t;-t\right)\\\overrightarrow{MC}=\left(-2-2t;-6-t\right)\end{matrix}\right.\) \(\Rightarrow\overrightarrow{MA}+\overrightarrow{MC}=\left(-2-4t;-6-2t\right)\)
Đặt \(T=\left|\overrightarrow{MA}+\overrightarrow{MC}\right|=\sqrt{\left(-2-4t\right)^2+\left(-6-2t\right)^2}=\sqrt{20\left(t+1\right)^2+20}\ge\sqrt{20}\)
Dấu "=" xảy ra khi \(t+1=0\Rightarrow t=-1\Rightarrow M\left(3;3\right)\)
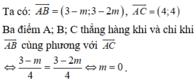

\(\overrightarrow{AM}=\left(m+5;2m\right)\)
\(\overrightarrow{AB}=\left(1;2\right)\)
Để A,M,B thẳng hàng thì \(\dfrac{m+5}{1}=\dfrac{2m}{2}\)
=>m+5=m(loại)