Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ta có pt đường cao kẻ từ B:(d1) x+3y-5=0
vì AC _|_ (d1) và AC đi qua C(-1; -2)
=> pt AC: 3(x+1) -(y+2) =0
<=> 3x -y + 1=0
ta có A là giao điểm của AC và đg trung tuyến (d2) kẻ từ A
=> A là nghiệm của hệ:
{ 5x+y-9=0
{ 3x -y + 1=0
<=>
x=1 ; y=4
=> A( 1;4)
Vì B ∈ (d1) => B(5- 3y; y)
gọi I là trung điểm BC => I ∈ (d2)
Vì I là trung điểm BC
=>
{ 2xI = xB + xC
{ 2yI = yB + yC
<=>
{ xI= (5-3y-1)/2 = (4-3y)/2
{ yI= (y -2)/2
Vì I ∈ (d2)
=> 5(4-3y)/2 + (y -2)/2 -9 =0
<=> y= 0
=> B( 5; 0)
Vậy A( 1;4) và B( 5; 0)
Ta có pt đường cao kẻ từ B: (d1) x+3y-5=0
Vì AC _|_ (d1) và AC đi qua C(-1; -2)
=> pt AC: 3(x+1) -(y+2) =0
<=> 3x -y + 1=0
Ta có A là giao điểm của AC và đường trung tuyến (d2) kẻ từ A
=> A là nghiệm của hệ:
{ 5x+y-9=0
{ 3x -y + 1=0
<=>
x=1 ; y=4
=> A( 1;4)
Vì B ∈ (d1) => B(5- 3y; y)
Gọi I là trung điểm BC => I ∈ (d2)
Vì I là trung điểm BC
=>
{ 2xI = xB + xC
{ 2yI = yB + yC
<=>
{ xI= (5-3y-1)/2 = (4-3y)/2
{ yI= (y -2)/2
Vì I ∈ (d2)
=> 5(4-3y)/2 + (y -2)/2 -9 =0
<=> y= 0
=> B( 5; 0)
Vậy A( 1;4) và B( 5; 0)







Đáp án A
Phân tích.
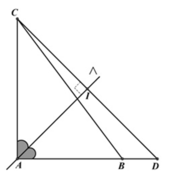
- Ta thấy A thuộc đường phân giác trong góc A: x - 3 y + 5 = 0 giờ chỉ cần viết được phương trình AC là tìm được A.
- Trên AC đã có một điểm N, cần tìm thêm một điểm nữa. Chú ý khi lấy M’ đối xứng với M qua phân giác trong ta có M’ thuộc cạnh AC.
- Tìm M’ viết được phương trình AC từ đó suy ra A. Có A, M viết được phương trình AB.
- Gọi B, C và tham số hóa dựa vào B thuộc AB, C thuộc AC. Áp dụng công thức trọng tâm sẽ tìm ra được tọa độ B, C.
Hướng dẫn giải.
Gọi M ' ∈ A C là điểm đối xứng của M qua phân giác trong góc A, gọi I là giao điểm của MM' với phân giác trong góc A → I là trung điểm MM’.
Phương trình MM’ là: 3 x + y - 11 = 0
Toạ độ điểm I là nghiệm của hệ:
M’ đối xứng với M qua
Đường thẳng AC qua N và M’ nên có phương trình:
Tọa độ A là nghiệm của hệ:
Đường thẳng AB đi qua A, M nên có phương trình:
x + y - 3 = 0
Gọi
Do G là trọng tâm tam giác ABC nên ta có:
Vậy tọa độ các đỉnh của tam giác ABC là: