Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\left(d_1\right):y=-x+1\)
\(\left(d_2\right):y=x-1\)
\(\left(d_3\right):y=\dfrac{k+1}{1-k}x+\dfrac{k+1}{k-1}\)
a) Để (d1) và (d3) vuông góc với nhau:
\(\Leftrightarrow\left(-1\right)\left(\dfrac{k+1}{1-k}\right)=-1\)\(\Leftrightarrow k=0\)(thỏa)
Vậy k=0
b)Giao điểm của (d1) và (d2) là nghiệm của hệ \(\left\{{}\begin{matrix}y=-x+1\\y=x-1\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}y=0\\x=1\end{matrix}\right.\)
Để (d1);(d2);(d3) đồng quy\(\Leftrightarrow\) (d3) đi qua điểm (1;0)
\(\Rightarrow0=\dfrac{k+1}{1-k}.1+\dfrac{k+1}{k-1}\)\(\Leftrightarrow0=0\)(lđ)
Vậy với mọi k thì (d1);d2);(d3) luôn cắt nhau tại một điểm
c)Gỉa sử \(M\left(x_0;y_0\right)\) là điểm cố định mà (d3) luôn đi qua
Khi đó \(\left(k+1\right)x_0+\left(k-1\right)y_0=k+1\) luôn đúng với mọi k
\(\Leftrightarrow k\left(x_0+y_0-1\right)+x_0-y_0-1=0\) luôn đúng với mọi k
\(\Leftrightarrow\left\{{}\begin{matrix}x_0+y_0-1=0\\x_0-y_0-1=0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x_0=2\\y_0=1\end{matrix}\right.\)
Vậy \(M\left(2;1\right)\) là điểm cố định mà (d3) luôn đi qua.

Tọa độ giao điểm của đường thẳng (d1) và (d2) là:
\(\left\{{}\begin{matrix}-2x+5y-8=0\\x+2y-5=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=2\end{matrix}\right.\)
Để 3 đường thẳng trên đồng qua thì:
\(\left(m^2-1\right)x+3y-5-2m=0\\ \Leftrightarrow\left(m^2-1\right).1+3.2-5-2m=0\\ \Leftrightarrow m^2-1+6-5-2m=0\\ \Leftrightarrow m^2-2m=0\\ \Leftrightarrow m\left(m-2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}m=0\\m=2\end{matrix}\right.\)
Tọa độ giao điểm của (d1) và (d2) là:
\(\left\{{}\begin{matrix}-2x+5y-8=x+2y-5\\x+2y-5=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-x+y=1\\x+2y=5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=2\\x=1\end{matrix}\right.\)
Thay x=1 và y=2 vào (d3), ta được:
\(m^2-1+3\cdot2-5-2m=0\)
\(\Leftrightarrow m\left(m-2\right)=0\)
hay \(m\in\left\{0;2\right\}\)

Tọa độ giao điểm của (d1) và (d2) là nghiệm của hệ phương trình sau:
\(\left\{{}\begin{matrix}x+2=-2\\y=-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-4\\y=-2\end{matrix}\right.\)
Thay x=-4 và y=-2 vào (d3), ta được:
\(-4\left(k+1\right)+k=-2\)
=>\(-4k-4+k=-2\)
=>-3k=-2+4=2
=>\(k=\dfrac{2}{-3}=-\dfrac{2}{3}\)

\(PT\text{ hoành độ giao điểm }\left(d_1\right);\left(d_2\right)\\ 4x+4=2x+2\Leftrightarrow x=-1\Leftrightarrow y=0\Leftrightarrow A\left(-1;0\right)\\ \text{Đồng quy }\Leftrightarrow A\left(-1;0\right)\in\left(d_3\right)\Leftrightarrow-3m-5+m-1=0\Leftrightarrow-2m-6=0\Leftrightarrow m=-3\)

a: 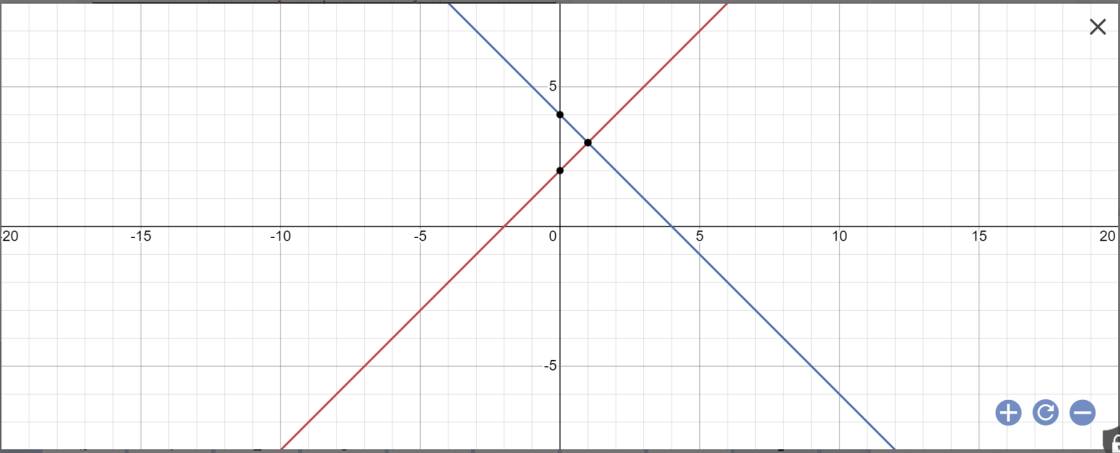
b: Tọa độ giao điểm của (d1) và (d2) là:
\(\left\{{}\begin{matrix}x+2=-x+4\\y=x+2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x=2\\y=x+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=1+2=3\end{matrix}\right.\)
Thay x=1 và y=3 vào (d3), ta được:
\(1\cdot m+m=3\)
=>2m=3
=>\(m=\dfrac{3}{2}\)

a, (d1) y = -x + 1
(d3) y = \(\dfrac{k+1}{1-k}\) x -\(\dfrac{k+1}{1-k}\) ĐK k \(\ne\) 1
Để d1 \(\perp\) d3 \(\Leftrightarrow\) -1.\(\dfrac{k+1}{1-k}\) = -1 \(\Rightarrow\)k+1=1-k
\(\Rightarrow\) k = 0 (TM)
b, Xét pt hoành độ giao điểm của d1 và d2
x-1 = 1-x \(\Leftrightarrow\) x= 1 \(\Rightarrow\) y = 0
vậy A(1;0)
Để d1 , d2 và d3 đồng quy \(\Leftrightarrow\) A thuộc d3
thay A(1;0) vào d3 đc
0 = 0.k
Vậy vs mọi k\(\ne\) 1 thì d1,d2,d3 .....
c, Gọi B(xB;yB) là điểm cố định d3 luôn đi qua với mọi k khác 1
Ta có
k.xB+xB+k.yB-yB-k-1=0 đúng với mọi k\(\ne\)1
\(\Leftrightarrow\)k(xB+yB-1)+(xB-yB-1) =0 đúng với ...
\(\Rightarrow\left\{{}\begin{matrix}x_B+y_B=1\\x_B-y_B=1\end{matrix}\right.\) \(\Leftrightarrow\) \(\left\{{}\begin{matrix}x_B=1\\y_B=0\end{matrix}\right.\)
=> B(1;0) ...
Nguyễn Việt Lâm, Phùng Khánh Linh, Thiên Hàn, Khánh Như Trương Ngọc, Trần Trung Nguyên, Bonking, Nguyễn Thị Thảo Vy, KHUÊ VŨ, Phạm Tiến, Nigou Nguyễn , Mysterious Person, Mashiro Shiina, Nguyễn Thanh Hằng, Aki Tsuki, ...

1. a) Để hs trên là hs bậc nhất khi và chỉ khi a>0 --> 3+2k>0 --> k >\(\frac{-3}{2}\)
b) Vì đths cắt trục tung tại điểm có tung độ = 5 --> x=0, y=5
Thay y=5 và x=0 vào hs và tìm k
2. a) Tự vẽ
b) Hệ số góc k=\(\frac{-a}{b}=\frac{-2}{4}=\frac{-1}{2}\)
c) Phương trình hoành độ giao điểm là:\(2x+4=-x-2\)(tìm x rồi thay x vào 1 trong 2 pt --> tính y) (x=-2; y=0)
3. Vì 3 đg thẳng đồng quy -->d1 giao d2 giao d3 tại 1 điểm (giao kí hiệu là chữ U ngược)
Tính tọa độ giao điểm của d1 và d2 --> x=2;y=1
Điểm (2;1) thuộc d3 --> Thay x=2 và y=1 vào d3 -->m=3

1: Để hai đường song song thì m+3=2
hay m=-1
3: Tọa độ của điểm A là:
\(\left\{{}\begin{matrix}y_A=0\\2x+4=0\end{matrix}\right.\Leftrightarrow A\left(-2;0\right)\)
Tọa độ điểm B là:
\(\left\{{}\begin{matrix}y_B=0\\-x+4=0\end{matrix}\right.\Leftrightarrow B\left(4;0\right)\)
 help me pls
help me pls