
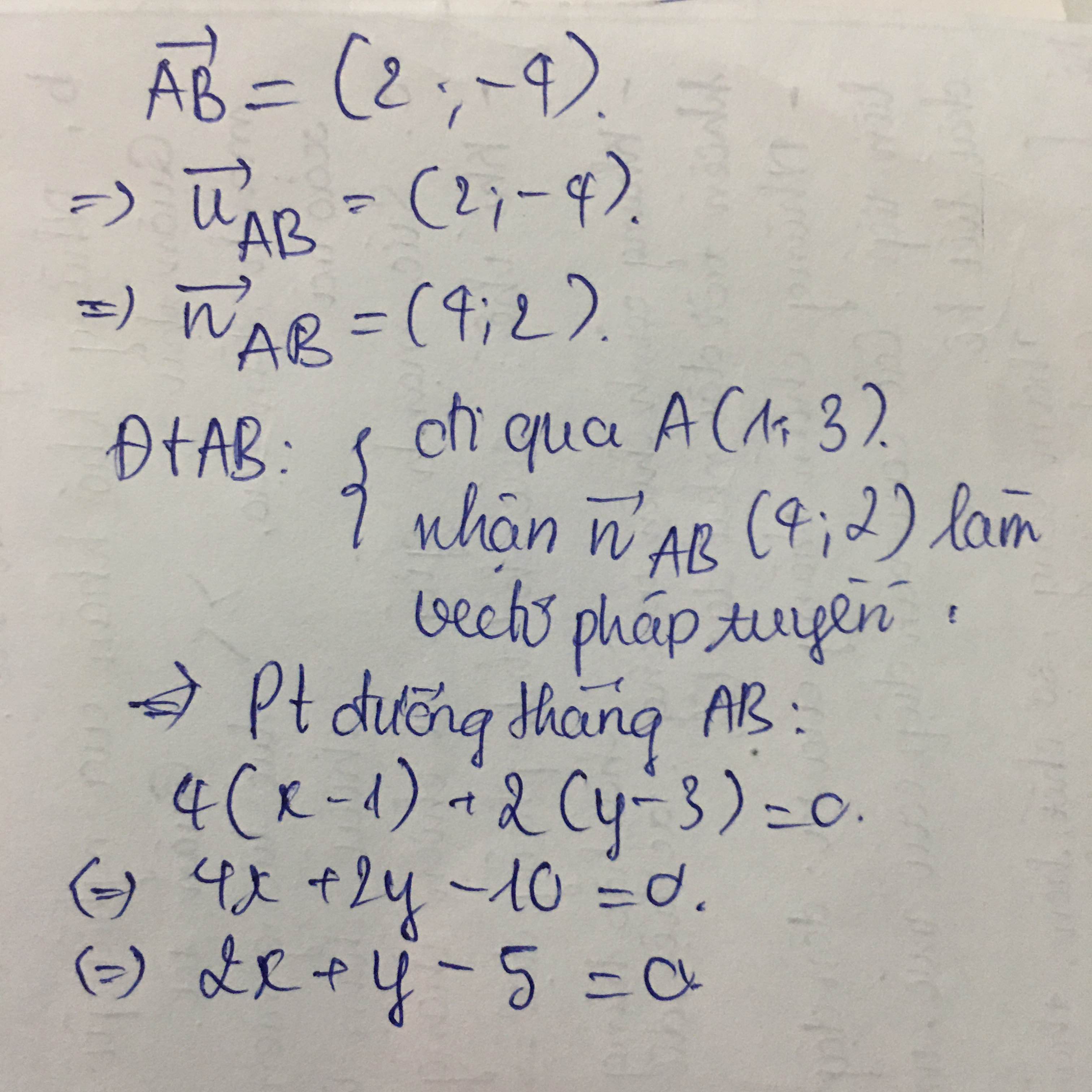
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

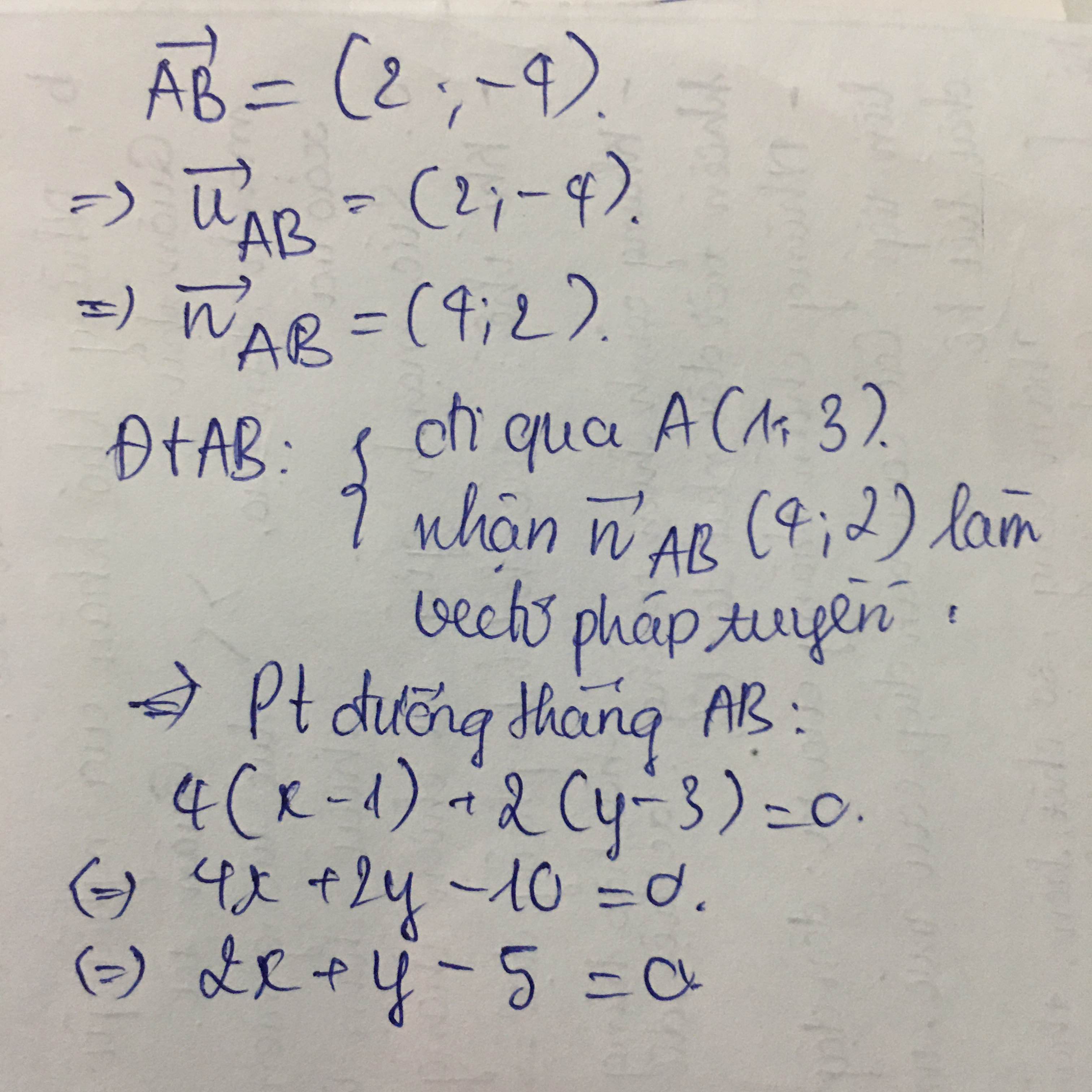

a: A(1;2); B(2;1)
=>\(\overrightarrow{AB}=\left(1;-1\right)\)
=>VTPT là (1;1)
Phương trình đường thẳng AB là:
1(x-1)+2(y-1)=0
=>x-1+2y-2=0
=>x+2y-3=0
b:
M(1;3); Δ: 3x+4y+10=0
Khoảng cách từ M đến Δ là:
\(d\left(M;\text{Δ}\right)=\dfrac{\left|1\cdot3+3\cdot4+10\right|}{\sqrt{3^2+4^2}}=\dfrac{\left|3+12+10\right|}{5}=5\)

Câu 4:
Tọa độtâm I là;
x=(4+2)/2=3 và y=(-3+1)/2=-1
I(3;-1); A(4;-3)
IA=căn (4-3)^2+(-3+1)^2=căn 5
=>(C): (x-3)^2+(y+1)^2=5
Câu 3:
vecto AB=(2;3)
PTTS là:
x=1+2t và y=-2+3t

a: (Δ)//d nên Δ: -x+2y+c=0
=>VTPT là (-1;2)
=>VTCP là (2;1)
PTTS là:
x=3+2t và y=1+t
b: (d): -x+2y+1=0
=>Δ: 2x+y+c=0
Thay x=4 và y=-2 vào Δ, ta được:
c+8-2=0
=>c=-6

a: vecto AB=(6;-4)
PTTS là:
x=-6+6t và y=3-4t
b: Vì (d) vuông góc AB nên (d) có VTPT là (3;-2)
Phương trình(d) là:
3(x-3)+(-2)(y-2)=0
=>3x-9-2y+4=0
=>3x-2y-5=0

a.
\(\overrightarrow{AB}=\left(3;-4\right)\Rightarrow\) đường thẳng AB nhận (4;3) là 1 vtpt
Phương trình AB:
\(4\left(x-2\right)+3\left(y-5\right)=0\Leftrightarrow4x+3y-23=0\)b.
Do d vuông góc delta nên d nhận (4;-3) là 1 vtpt
Phương trình d có dạng: \(4x-3y+c=0\)
\(d\left(B;d\right)=\dfrac{\left|4.5-3.1+c\right|}{\sqrt{4^2+\left(-3\right)^2}}=\dfrac{1}{5}\)
\(\Rightarrow\left|c+17\right|=1\Rightarrow\left[{}\begin{matrix}c=-16\\c=-18\end{matrix}\right.\)
Có 2 đường thẳng d thỏa mãn: \(\left[{}\begin{matrix}4x-3y-16=0\\4x-3y-18=0\end{matrix}\right.\)

I nằm trên d nên I(x;-2x-5)
IA=IB=R
=>(x-1)^2+(-2x-5+3)^2=(x+3)^2+(-2x-5-1)^2
=>x^2-2x+1+4x^2+8x+4=x^2+6x+9+4x^2+24x+36
=>6x+5=30x+45
=>-24x=40
=>x=-5/3
=>I(-5/3;-5/3)
A(1;-3)
=>R=4/3*căn 5
=>(C): (x+5/3)^2+(y+5/3)^2=80/9

1: Gọi I(0,y) là tâm cần tìm
Theo đề, ta có: IA=IB
=>\(\left(0-3\right)^2+\left(5-y\right)^2=\left(1-0\right)^2+\left(-7-y\right)^2\)
=>y^2-10y+25+9=y^2+14y+49+1
=>-10y+34=14y+50
=>-4y=16
=>y=-4
=>I(0;-4)
=>(x-0)^2+(y+4)^2=IA^2=90
2: Gọi (d1) là đường thẳng cần tìm
Vì (d1)//(d) nên (d1): 4x+3y+c=0
Theo đề, ta có: d(I;(d1))=3 căn 10
=>\(\dfrac{\left|0\cdot4+\left(-4\right)\cdot3+c\right|}{5}=3\sqrt{10}\)
=>|c-12|=15căn 10
=>\(\left[{}\begin{matrix}c=15\sqrt{10}+12\\c=-15\sqrt{10}+12\end{matrix}\right.\)