Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.

Mặt phẳng (α) vuông góc với 2 mặt phẳng (P) và (Q) nên có một VTPT là
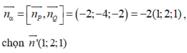
Phương trình mặt phẳng (α) là:
1(x - 2) + 2(y + 1) + 1.(z - 5) = 0 hay x + 2y + z – 5 = 0

Đáp án B
Phương pháp:
![]()
![]()
Thay tọa độ điểm A vào phương trình mặt phẳng (P) và tìm hằng số m
Cách giải:
![]()
![]()
![]()
![]()
![]()
![]()
Mà (thỏa mãn)

Đáp án D
Ta có:
2 x - 4 y + 3 z - 24 = 0 ⇔ x 12 - y 6 + z 8 = 1
Do đó mặt phẳng (P) cắt các trục Ox; Oy; Oz lần lượt tại các điểm A(12; 0;0); B(0;-6;0); C(0;0;8). Khối đa diện cần tính thể tích là khối tứ diện OABC có OA, OB, OC đôi một vuông góc có độ dài OA=12; OB=6; OC=8
Do đó : V = 1 6 O A . O B . O C = 96 . Chọn D.

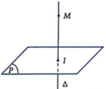
\(\overrightarrow{MI}=\left(2;-3;-3\right)\)
(P) tiếp xúc (I) tại M nên nhận (2;-3;-3) là 1 vtpt
Phương trình:
\(2\left(x-1\right)-3\left(y-4\right)-3\left(z-2\right)=0\)
\(\Leftrightarrow2x-3y-3z+16=0\)

Đáp án B
Phương trình mặt phẳng (Q) có dạng: x - 2y - 3z + m = 0 (m ≠ 10).
Vì (Q) đi qua điểm A(2; -1; 0) nên ta có 2 + 2 + m = 0 <=> m = -4.
Vậy phương trình mặt phẳng (Q) là x - 2y - 3z -4 = 0 hay -x + 2y + 3z + 4 = 0.
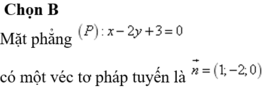
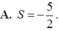
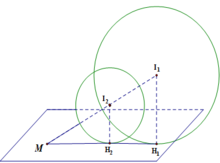



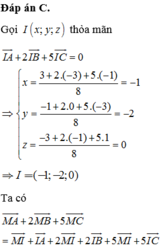

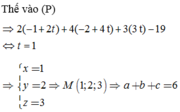


Đáp án C
Phương trình mặt phẳng đoạn chắn của (ABC) là
Do đó (ABC): 6x + 4y + 3z - 12 = 0