Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Phương pháp :
Gọi (Q): x + y + z + a = 0 (a≠3) là mặt phẳng song song với mặt phẳng (P).
Sử dụng công thức tính khoảng cách từ 1 điểm đến một mặt phẳng.
Cách giải :
Gọi (Q): x + y + z + a = 0 (a≠3) là mặt phẳng song song với mặt phẳng (P).
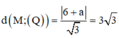

Với ![]()
![]()
Vậy không có mặt phẳng (Q) nào thỏa mãn điều kiện bài toán

Đáp án B.
Q / / P nên mặt phẳng (Q) có dạng:
2 x − 2 y + z + m = 0 với m ≠ − 5
Mặt phẳng (P) đi qua điểm M 1 ; 1 ; 5 . Theo đề:
d P , Q = 3 ⇔ d M , Q = 3 ⇔ 2.1 − 2.1 + 5 + m 2 2 + − 2 2 + 1 2 = 3 ⇔ m = 4 m = − 14 ⇔ Q : 2 x − 2 y + z + 4 = 0 Q : 2 x − 2 y + z − 14 = 0

Đáp án B.
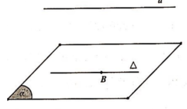
Dễ thấy d ⊥ α và − 1 ; − 2 ; − 3 ∈ α ⇒ d ⊂ α .
Ta có B = Δ ∩ Oxy ⇒ B a ; b ; 0 mà B ∈ Δ ⊂ α ⇒ 2 a + b − 2 = 0 (1).
Lại có d / / Δ ⇒ d d ; Δ = d B ; d = 3.
Đường thẳng d đi qua M 0 ; 0 ; − 1 , có u d → = 1 ; 2 ; 2 .
Do đó:
d B ; d = B M → ; u d → u d → = 2 b − 2 2 + 1 − 2 a 2 + 2 a − b 2 3 = 3 2
Từ (1), (2) suy ra:
a ; b = − 1 ; 4 → B − 1 ; 4 ; 0 a ; b = 2 ; − 2 → B 2 ; − 2 ; 0 .
Vậy A B = 7 2 .


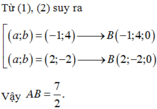
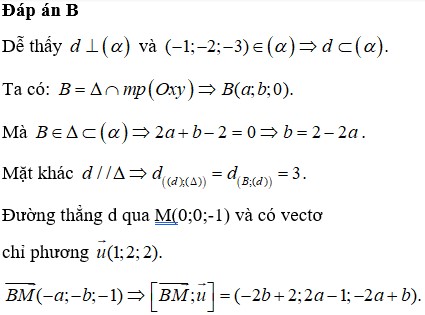
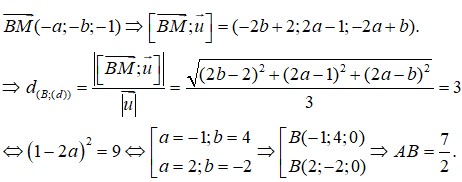


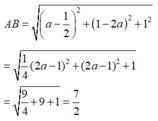


Đáp án D