Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
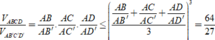
![]()
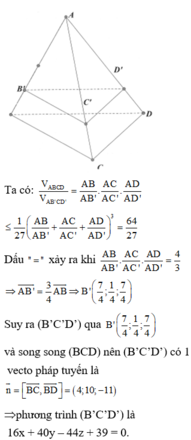
Dấu = xảy ra khi:![]()
Suy ra 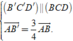
Ta có 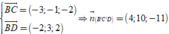
Mặt khác
![]()
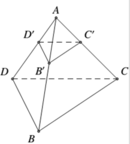
Vậy phương trình mặt phẳng (B' C' D') là ![]()

Chọn đáp án C
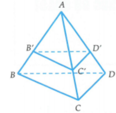
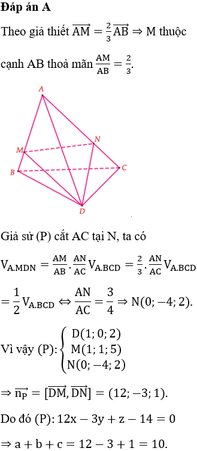
Áp dụng công thức tỉ số thể tích ta có:
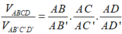
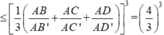
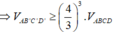
Suy ra thể tích tứ diện AB'C'D' nhỏ nhất khi
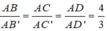
Khi đó A B ' ⇀ = 3 4 A B ⇀ và B ' C ' D ' / / B C D
⇒ Mặt phẳng B ' C ' D ' có một vec-tơ pháp tuyến là
![]()
Lại có
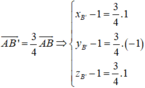
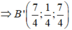
Phương trình mặt phẳng B ' C ' D '
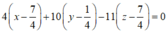
![]()

Đáp án B
 Gọi
A
=
∆
∩
P
;
d
=
P
∩
Q
Gọi
A
=
∆
∩
P
;
d
=
P
∩
Q
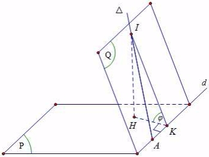
Lấy I ∈ ∆ ⇒ A ; I cố định, kẻ I H ⊥ P ; H K ⊥ d ⇒ P ; Q ^ = I K H ^ = φ
Do I A ≥ I K ⇒ sin φ = I H I K ≥ I H I A ⇒ φ m i n khi K ≡ A tức là I A ⊥ d ⇒ n Q → = u ∆ → ; u d →
Trong đó n ∆ ¯ = 1 ; - 2 ; - 2 ; u d ¯ = u ∆ ¯ ; u P ¯ = 3 ; 0 ; 3 = 3 1 ; 0 ; 1
Suy ra n Q ¯ = u ∆ ¯ ; u d ¯ = - 2 1 ; 1 ; - 1 , mặt khác (Q) chứa đường thẳng ∆ nên (Q) đi qua điểm (1;2;-1)
Do đó Q : x + y - z - 4 = 0 ⇒ A 4 ; 0 ; 0 , B ( 0 ; 4 ; 0 ) , C ( 0 ; 0 ; - 4 ) ⇒ V O . A B C = 64 6 = 32 3

Đáp án A
Phương trình mặt phẳng A B C : x a + y b + z c = 1
Vì I ∈ A B C ⇔ 1 a + 2 b + 3 c ≥ 3 6 a b c 3 ⇔ a b c ≥ 162
Thể tích khối tứ diện OABC được tính là V = O A . O B . O C 6 = a b c 6 ≥ 162 6 = 27
Dấu “=” xảy ra khi 1 a = 2 b = 3 c = 1 3 ⇒ a = 3 b = 6 c = 9
Kiểm tra thấy phương án A không đúng

Chọn D.
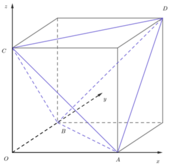
Phương pháp: Tứ diện ABCD có các cặp cạnh đối diện bằng nhau là tứ diện gần đều.
Cách giải: Theo giả thiết suy ra:
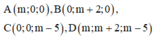
Theo tính chất của tứ diện gần đều tâm mặt cầu ngoại tiếp I của tứ diện ABCD là trung điểm OD
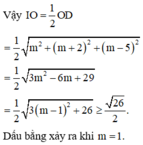


Đáp án D