Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C.
Phương pháp:
- Viết phương trình mặt phẳng α .
- Tìm tọa độ giao điểm B, C của α với trục Oy, Oz.
- Tính thể tích khối tứ diện vuông OABC: V = 1 6 . O A . O B . O C .
Cách giải:
Giả sử n → a ; b ; c , a 2 + b 2 + c 2 ≠ 0 là một vecto pháp tuyến của (P).
Vì α đi qua A 2 ; 0 ; 0 nên PTTQ của (P):
a x − 2 + b y − 0 + c z − 0 = 0
⇔ a x + b y + c z − 2 a = 0.
Vì α vuông góc với α nên n → a ; b ; c vuông góc với n 1 → 0 ; 2 ; − 1 .
Khi đó,
0. a + 2. b + − 1 . c = 0 ⇔ c = 2 b
⇒ α : a x + b y + 2 b z − 2 a = 0
d O ; α = 4 3 ⇔ − 2 a a 2 + b 2 + 4 b 2 = 4 3 ⇔ 6 a 2 = 16 a 2 + 5 b 2 ⇔ a 2 = 4 b 2 ⇔ a = 2 b a = − 2 b
Cho
b = 1 ⇒ a = 2 a = − 2 ⇒ n → 2 ; 1 ; 2 n → − 2 ; 1 ; 2 ⇒ α : 2 x + y + 2 z − 4 = 0 α : − 2 x + y + 2 z + 4 = 0
+ ) α : 2 x + y + 2 z − 4 = 0 ⇒ B 0 ; 4 ; 0 , C 0 ; 0 ; 2 ⇒ V O A B C = 1 6 . 2 . 4 . 2 = 8 3
+ ) α : − 2 x + y + 2 z + 4 = 0 ⇒ B 0 ; − 4 ; 0 , C 0 ; 0 ; − 2 ⇒ V O A B C = 1 6 . 2 . − 4 . − 2 = 8 3
Vậy thể tích khối tứ diện OABC là 8 3 .

Phương pháp:
Gọi tọa độ các điểm A, B, C.
Lập phương trình mặt phẳng đi qua H và cắt các trục Ox, Oy, Oz bằng phương trình đoạn chắn.
Từ đó tìm được các điểm A, B, C. Từ đó tính được bán kính mặt cầu ngoại tiếp tứ diện OABC.
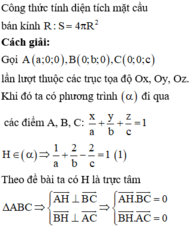
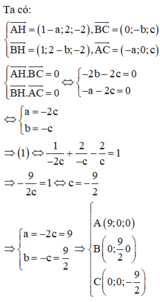
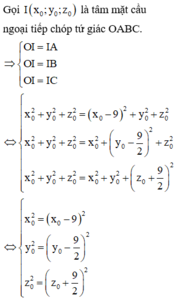
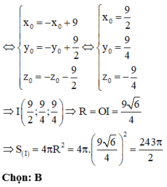






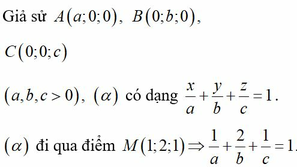
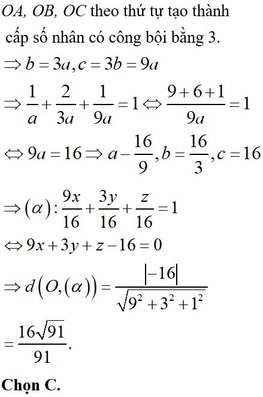

Đáp án C