Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn A
Gọi A(a;0;0);B(0;b;0);C(0;0;c)
Phương trình mặt phẳng (P) có dạng:
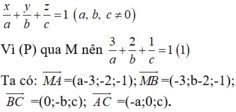
Vì M là trực tâm của tam giác ABC nên:
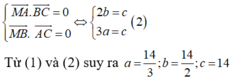
Khi đó phương trình (P): 3x+2y+z-14=0.
Vậy mặt phẳng song song với (P) là: 3x+2y+z+14=0.
Chọn B.
là giao điểm của mặt phẳng (α) các trục Ox, Oy, Oz
Phương trình mặt phẳng
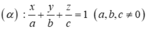
Ta có G là trọng tâm tam giác ABC
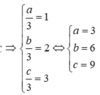
Đáp án B
Vì OA, OB, OC đôi một vuông góc và M là trực tâm tam giác ABC => OM ⊥ (ABC)
Suy ra mp(ABC) nhận O M → làm véc tơ pháp tuyến và đi qua điểm M(1;2;3)
Vậy phương trình mp(P):
<=> x +2y+3z -14=0
Đáp án D
Ta có: OA → OB, OC => OA → (OBC) => OA → BC
Mặt khác vì AM → BC (M là trực tâm tam giác ABC) nên ta suy ra BC → (OAM) => BC → OM
Chứng minh tương tự ta được AC → OM. Do đó OM → (ABC). Ta chọn: n p → = OM → = (1; -2; 3)
Từ đó suy ra phương trình của mặt phẳng (P) là:
1(x - 1) - 2(y + 2) + 3(z - 3) = 0 ⇔ x - 2y + 3z - 14 = 0
Đáp án D
Ta có OA ⊥ OB, OC => OA ⊥ (OBC) => OA ⊥ BC.
Mặt khác ta có AM ⊥ BC nên ta suy ra BC ⊥ (OAM) => BC ⊥ OM
Chứng minh tương tự ta được AC ⊥ OM. Do đó OM ⊥ (ABC).
Ta chọn n P → = OM → = (1; 2; 2). Từ đó suy ra phương trình của mặt phẳng (P) là:
1(x - 1) + 2(y - 2) + 2(z - 2) = 0 <=> x + 2y + 2z - 9 = 0
Chọn D
Chọn D
Xét tứ diện OABC có OA, OB, OC đôi một vuông góc nên nếu M là trực tâm tam giác ABC thì OM ⊥ (ABC)
Khi đó phương trình mặt phẳng (ABC) là: 2 (x-2)+ (y-1)+5 (z-5) = 0 ó 2x + y + 5z – 30 = 0.
Vậy khoảng cách từ điểm I (1;2;3) đến mặt phẳng (P) là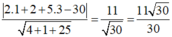 
Đáp án D
Kiến thức: Chóp tam giác có 3 cạnh bên đôi một vuông góc với nhau thì hình chiếu của đỉnh trên mặt đáy trùng với trực tâm của đáy.
Chóp O.ABC có các cạnh OA, OB, OC đôi một vuông góc với nhau, M(2;1;5) là trực tâm của tam giác ABC
vậy (P) nhận O M → =(2;1;5) làm một vectơ pháp tuyến.
=> Phương trình mặt phẳng (P) là: 2(x-2)+y-1+5(z-5)=0
<=> 2x+y+5z-30=0
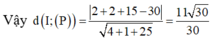
Đáp án B
Phương trình của mặt phẳng (P) là 3(x-0)+2(y-0)+1(z-0)=0<=> 3x+2y+z=0.
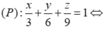
Đáp án A.
Gọi:
Phương trình mặt phẳng (P) có dạng:
Vì M là trực tâm của tam giác ABC nên