
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

![]()

Gọi B(x;y), ta có \(OA\perp OC\) nên OABC là hình chữ nhật =>\(\overrightarrow{AB}=\overrightarrow{OC}\) \(\Leftrightarrow\begin{cases}x-2=0\\y-0=4\\z-0=0\end{cases}\) \(\Rightarrow B\left(2;4;0\right)\)
Ta có \(\overrightarrow{OB}=\left(2;4;0\right);\overrightarrow{OD}=\left(0;0;4\right);\overrightarrow{CB}=\left(2;0;0\right);\overrightarrow{CD}=\left(0;-4;4\right)\)
Do đó \(\overrightarrow{OB}.\overrightarrow{OD}=0\) và \(\overrightarrow{CB}.\overrightarrow{CD}=0\Rightarrow\widehat{BOD}=\widehat{BCD}=90^0\)
Suy ra mặt cầu đi qua 4 điểm O, B, C, D có tâm I là trung điểm của BD, bán kính R=OI
Ta có \(I\left(1;2;2\right);R=OI=\sqrt{1+2^2+2^2}=3\)
Do đó mặt cầu (S) có phương trình : \(\left(x-1\right)^2+\left(y-2\right)^2+\left(z-2\right)^2=9\)

Chọn D
Ta có: A (2; 0; 0), B (0; 4; 0), C (0; 0 ;6).
Thể tích khối tứ diện OABC là:
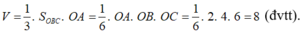

Đáp án C.
Vì OA = 1, OB = 2, OC = 3 và đôi một vuông góc
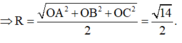

Đáp án B
Phương pháp: (P) cách đều B, C
![]()
TH1: BC//(P)
TH2: I ∈ (P)với I là trung điểm của BC.
Cách giải:
![]()
(P) cách đều B, C
![]()
TH1: BC//(P)
![]()
=> (P) đi qua O và nhận b → = ( 6 ; - 3 ; - 4 ) là 1 VTPT
![]()
TH2: I ∈ (P) với I là trung điểm của BC.
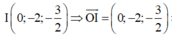
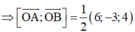
![]()
Dựa vào các đáp án ta chọn được đáp án B.