Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Vì OA, OB, OC đôi một vuông góc với nhau 1 d 2 = 1 O A 2 + 1 O B 2 + 1 O C 2
Với d là khoảng cách từ O -> (ABC) suy ra 1 d 2 = 1 a 2 + 1 b 2 + 1 c 2
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức, ta có x 2 a + y 2 b + z 2 c ≥ x + y + z 2 a + b + c
Vậy d m a x = 1 3

Đáp án D
Phương pháp:
- Phương trình đoạn chắn của mặt phẳng đi qua 3 điểm A(a;0;0), B(0;b;0), C(0;0;c) với a, b, c khác 0
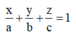
- Sử dụng bất đẳng thức
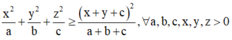
Đẳng thức xảy ra khi và chỉ khi
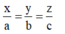
Cách giải:
![]()
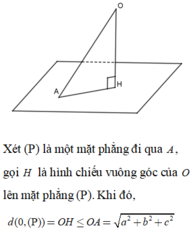
Mặt phẳng (ABC) có phương trình:
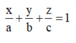
Khoảng cách từ O đến (ABC):
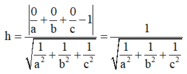
Ta có
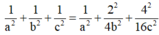
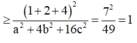
Dấu “=” xảy ra khi và chỉ khi:
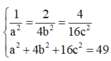
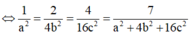
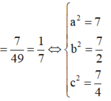
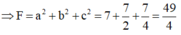

Đáp án A
Sử dụng phương trình mặt phẳng theo đoạn chắn, ta có phương trình mặt phẳng
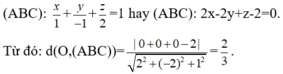

Đáp án D
Phương pháp: Sử dụng công thức tính khoảng cách từ 1 điểm đến một mặt phẳng.
Cách giải:
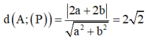
![]()
![]()

\(\left\{{}\begin{matrix}a+8-c+d=0\\\dfrac{\left|a-8+2c+d\right|}{\sqrt{a^2+16+c^2}}=5\end{matrix}\right.\)
\(\Rightarrow\left(3c-16\right)^2=25\left(a^2+c^2+16\right)\)
\(\Rightarrow25a^2+16c^2+96c+144=0\)
\(\Rightarrow25a^2+16\left(c+3\right)^2=0\Rightarrow\left\{{}\begin{matrix}a=0\\c=-3\end{matrix}\right.\)
\(\Rightarrow d=c-a-8=-11\)
\(\Rightarrow a+c+d=-14\)


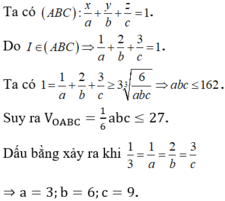
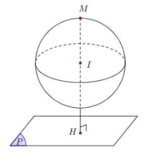

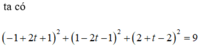
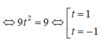
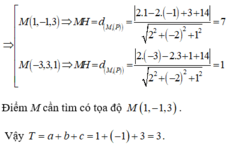
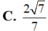
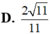
Đáp án B