Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hàm số ở câu a) \(y = 9{x^2} + 5x + 4\) là hàm số bậc hai với \(a = 9,b = 5,c = 4\)
Hàm số ở câu b), c) không phải là hàm số bậc hai vì chứa \({x^3}\)
Hàm số ở câu d) \(y = 5{x^2} + \sqrt x + 2\) không phải là hàm số bậc hai vì chứa \(\sqrt x \)

1: \(f\left(-x\right)=\left(-x\right)^2=x^2\)
Vậy: Hàm số này chẵn

Bài 1:
\(f\left(-x\right)=\left|\left(-x\right)^3+x\right|=\left|-x^3+x\right|=\left|-\left(x^3-x\right)\right|=\left|x^3-x\right|=f\left(x\right)\)
Vậy hàm số chẵn
Bài 2:
\(f\left(4\right)=4-3=1\\ f\left(-1\right)=2.1+1-3=0\\ b,\text{Thay }x=4;y=1\Leftrightarrow4-3=1\left(\text{đúng}\right)\\ \Leftrightarrow A\left(4;1\right)\in\left(C\right)\\ \text{Thay }x=-1;y=-4\Leftrightarrow2\left(-1\right)^2+1-3=-4\left(\text{vô lí}\right)\\ \Leftrightarrow B\left(-1;-4\right)\notin\left(C\right)\)

a)
1. Khởi động phần mềm đã cài đặt hoặc truy cập vào trang web: https://www.geogebra.org để sử dụng phiên bản online
2. Nhập phương trình bậc hai theo cú pháp y=-x^2+4x-3 vào vùng nhập lệnh như hình bên
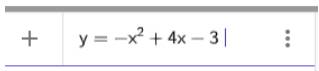
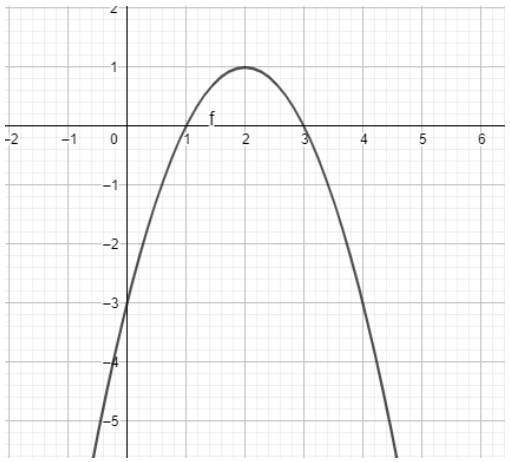
Ta có ngay parabol trên vùng làm việc như hình dưới:
b)
1. Khởi động phần mềm đã cài đặt hoặc truy cập vào trang web: https://www.geogebra.org để sử dụng phiên bản online
2. Nhập phương trình bậc hai theo cú pháp y=x^2+2 vào vùng nhập lệnh như hình bên
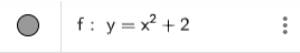
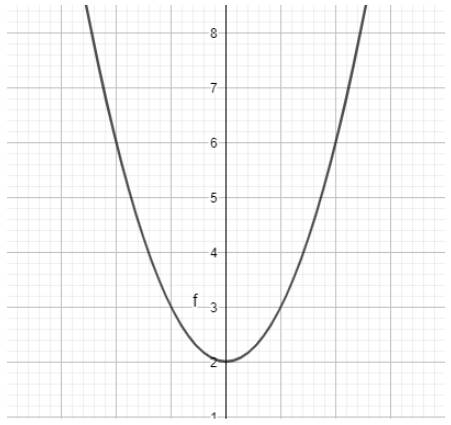
Ta có ngay parabol trên vùng làm việc như hình dưới:
c)
1. Khởi động phần mềm đã cài đặt hoặc truy cập vào trang web: https://www.geogebra.org để sử dụng phiên bản online
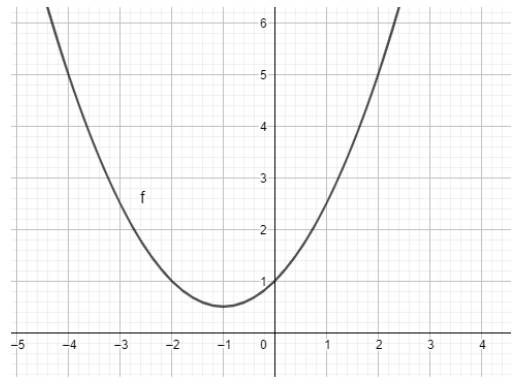
2. Nhập phương trình bậc hai theo cú pháp y=1/2x^2+x+1 vào vùng nhập lệnh như hình bên
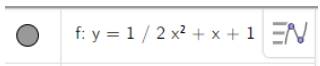
Ta có ngay parabol trên vùng làm việc như hình dưới:
d)
1. Khởi động phần mềm đã cài đặt hoặc truy cập vào trang web: https://www.geogebra.org để sử dụng phiên bản online
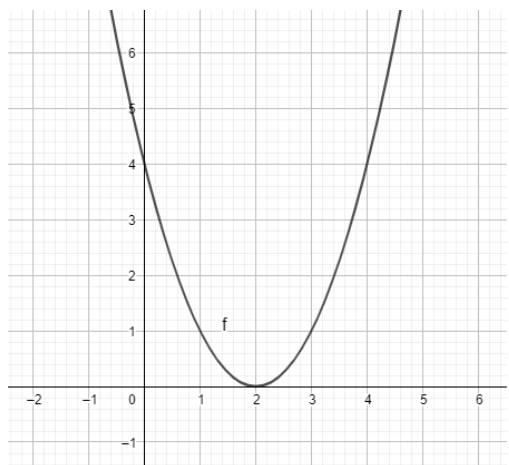
2. Nhập phương trình bậc hai theo cú pháp y=x^2-4x+4 vào vùng nhập lệnh như hình bên
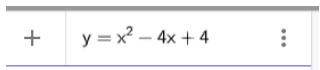
Ta có ngay parabol trên vùng làm việc như hình dưới:

e: \(f\left(-x\right)=\dfrac{\left(-x\right)^4+3\cdot\left(-x\right)^2-1}{\left(-x\right)^2-4}=\dfrac{x^4+3x^2-1}{x^2-4}=f\left(x\right)\)
Vậy: f(x) là hàm số chẵn
\(c,f\left(-x\right)=\sqrt{-2x+9}=-f\left(x\right)\)
Vậy hàm số lẻ
\(d,f\left(-x\right)=\left(-x-1\right)^{2010}+\left(1-x\right)^{2010}\\ =\left[-\left(x+1\right)\right]^{2010}+\left(x-1\right)^{2010}\\ =\left(x+1\right)^{2010}+\left(x-1\right)^{2010}=f\left(x\right)\)
Vậy hàm số chẵn
\(g,f\left(-x\right)=\sqrt[3]{-5x-3}+\sqrt[3]{-5x+3}\\ =-\sqrt[3]{5x+3}-\sqrt[3]{5x-3}=-f\left(x\right)\)
Vậy hàm số lẻ
\(h,f\left(-x\right)=\sqrt{3-x}-\sqrt{3+x}=-f\left(x\right)\)
Vậy hàm số lẻ

f(0)=2014=a.0^2+b.0+c=c => c=2014
f(1)=2015= a.1^2+b.1+c = a+b+c=a+b+2014 => a+b=2015-2014=1 (*)
f(-1)=2017=a.(-1)^2+b.(-1)+c= a-b+c=a-b+2014 =>a-b=2017-2014=3(**)
từ (*) và (**) ta có hệ pt và tính được a=2 và b= -1
=> f(-2) = 2.(-2)^2 + (-1).(-2) +2014=2024
F(0) = a.02 + b. 0 + c = 2014 => c = 2014
F(1) = a.12 + b. 1+ 2014 = 2015 => a + b = 2015 - 2014 = 1
F(-1) = a.(-1)2 + b.(-1) + 2014 = 2017 = > a - b = 2017 - 2014 = 3
Cộng vế cho vế ta được : 2a = 1 + 3 = 4=> a = 4/2 =2
thay a = 2 vào a + b = 1 ta có
2 + b = 1 => b = -1
F(x) = 2x2 - x + 2014
Vậy F(-2) = 2. (-2)2 - (-2) + 2014 = 2024
Đáp án C