Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Bị chặn trên vì \(u_n\le1,\forall n\in\mathbb{N}^{\circledast}\)
b) Bị chặn dưới vì \(u_n\ge2,\forall n\in\mathbb{N}^{\circledast}\)
c) Bị chặn dưới vì \(u_n\ge\sqrt{3},\forall n\in\mathbb{N}^{\circledast}\)
d) Bị chặn vì \(0< u_n\le\dfrac{1}{2},\forall n\in\mathbb{N}^{\circledast}\)


+) \(U_n=\sqrt{n^2+2}-n=\frac{2}{\sqrt{n^2+2}+n}\)
\(U_{n+1}=\sqrt{\left(n+1\right)^2+2}-\left(n+1\right)=\frac{2}{\sqrt{\left(n+1\right)^2+2}+n+1}\)
Vì \(\frac{2}{\sqrt{n^2+2}+n}>\frac{2}{\sqrt{\left(n+1\right)^2+2}+n+1}\)với mọi số tự nhiên n
=> \(U_n>U_{n+1}\)với mọi số tự nhiên n
=> \(U_n\) là dãy giảm.
+) Ta có: \(\sqrt{n^2+2}-n\le\sqrt{\left(n+\sqrt{2}\right)^2}-n=\sqrt{2}\)với mọi số tự nhiên n
=> \(U_n\) là dãy bị chặn

a) Ta có: \(n \ge 1\; \Rightarrow n - 1 \ge 0\; \Rightarrow {u_n} \ge 0,\;\forall \;n \in {N^*}\;\)
Do đó, \(\left( {{u_n}} \right)\) bị chặn dưới bởi 0.
\(\left( {{u_n}} \right)\) không bị chặn trên vì không tồn tại số M nào để \(n - 1 < M,\;\forall \;n \in {N^*}\).
b) Ta có:
\(\begin{array}{l}\forall n \in {N^*},{u_n} = \frac{{n + 1}}{{n + 2}} > 0.\\{u_n} = \frac{{n + 1}}{{n + 2}} = \frac{{n + 2 - 1}}{{n + 2}} = 1 - \frac{1}{{n + 2}} < 1,\forall n \in {N^*}\\ \Rightarrow 0 < {u_n} < 1\end{array}\)
Vậy \(\left( {{u_n}} \right)\) bị chặn.
c) Ta có:
\( - 1 < \sin n < 1\)
\( \Rightarrow - 1 < {u_n} < 1,\forall n \in {N^*}\)
Vậy \(\left( {{u_n}} \right)\) bị chặn.
d) Ta có:
Nếu n chẵn, \({u_n} = - {n^2} < 0\), \(\forall n \in {N^*}\).
Nếu n lẻ, \({u_n} = {n^2} > 0\), \(\forall n \in {N^*}\).
Vậy \(\left( {{u_n}} \right)\) không bị chặn.

a) Ta có:
\(\begin{array}{l}{n^2} \ge 1\,\,\,\forall n \in {\mathbb{N}^*}\\ \Leftrightarrow {n^2} + 2 \ge 3\,\,\,\forall n \in {\mathbb{N}^*}\end{array}\)
Dãy số bị chặn dưới
b) Ta có:
\(\begin{array}{l} - 2n \ge - 2\,\,\,\forall n \in {\mathbb{N}^*}\\ \Leftrightarrow - 2n + 1 \ge - 1\,\,\,\forall n \in {\mathbb{N}^*}\end{array}\)
Dãy số bị chặn dưới
c) Ta có:
\(\begin{array}{l}{n^2} \ge 1\,\,\,\forall n \in {\mathbb{N}^*}\\ \Leftrightarrow {n^2} + n \ge 2\,\,\,\forall n \in {\mathbb{N}^*}\\ \Leftrightarrow 0 \le \frac{1}{{{n^2} + n}} \le \frac{1}{2}\,\,\,\forall n \in {\mathbb{N}^*}\end{array}\)
Dãy số bị chặn

Ta có : 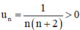 ∀ n ≥ 1.
∀ n ≥ 1.
⇒ (un) bị chặn dưới
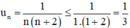 ∀ n ≥ 1.
∀ n ≥ 1.
⇒ (un) bị chặn trên.
Vậy (un) là dãy bị chặn.

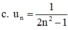
+ Ta có : 2n2 – 1 > 0 ∀ n ∈ N*
⇒ 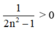 ∀ n ∈ N*.
∀ n ∈ N*.
⇒ (un) bị chặn dưới.
+ 2n2 – 1 ≥ 2.1 – 1 = 1
⇒ 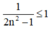 ∀ n ∈ N*
∀ n ∈ N*
⇒ (un) bị chặn trên.
Vậy (un) bị chặn.
un = 2n2 – 1
+ Với n ∈ N* ta có: n ≥ 1 và n2 ≥ 1
⇒ un = 2n2 – 1 ≥ 2.12 – 1 = 1.
⇒ un ≥ 1
⇒ dãy (un) bị chặn dưới ∀n ∈ N*.
+ (un) không bị chặn trên vì không có số M nào thỏa mãn:
un = 2n2 – 1 ≤ M ∀n ∈N*.
Vậy dãy số (un) bị chặn dưới và không bị chặn trên nên không bị chặn.