Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lấy một điểm thuộc d, chẳng hạn M = (0; 1).
Đường thẳng d 2 qua M vuông góc với có vectơ chỉ phương là v → = ( 2 ; − 3 ) .
Do đó phương trình của
d
2
là 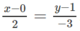 .
.
Gọi M' là giao của d 1 với d 2 thì tọa độ của nó phải thỏa mãn hệ phương trình:
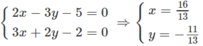
Từ đó suy ra
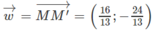

Đáp án A
Vectơ pháp tuyến của đường thẳng d là v → (1; –3). Ta có u → = k v → ( k ≠ 0 do d ≠ d ' )
⇔ u → ( k ; − 3 k ) . Áp dụng biểu thức tọa độ, ta có: x ' = k + x y ' = − 3 k + y ( trong đó x’; y’ thỏa mãn phương trình đường thẳng (d’))
=> k + x – 3( –3k + y) – 10 = 0 => x − 3 y + 10 k – 10 = 0 x − 3 y = 0 => k = 1

Phép vị tự tâm O(0; 0) tỉ số k = -5, biến M(x; y) thuộc d thành M’(x’, y’) thuộc d’ ⇒ O M ' → = - 5 O M →
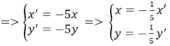
Thay vào phương trình d ta được:
2 . − 1 5 x ' + 3. − 1 5 y ' − 4 = 0 ⇔ − 2 5 x ' + − 3 5 y ' − 4 = 0 ⇔ 2 x ' + 3 y ' + 20 = 0
⇒ phương trình của d’ là 2x + 3y + 20 = 0
Đáp án D

