Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: | 2 + z | 2 < | 2 - z | 2
⇔ | 2 + x + iy | 2 < | 2 - x - iy | 2
⇔ 2 + x 2 + y 2 < 2 - x 2 + - y 2
⇔ x < 0
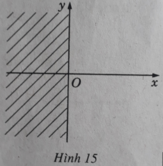
Đó là tập hợp các số phức có phần thực nhỏ hơn 0, tức là nửa trái của mặt phẳng tọa độ không kể trục Oy.

Chọn C.
Đặt ![]() ;
;
suy ra ![]()
Từ giả thiết, ta có:
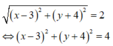
Tập hợp điểm biểu diễn các số phức z là đường tròn tâm I(3;-4) bán kính R=2.

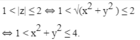
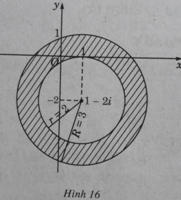
Vậy tập hợp điểm M là hình vành khăn tâm O, bán kính đường tròn nhỏ bằng 1,đường tròn lớn bằng 2, không kể các điểm thuộc đường tròn nhỏ.
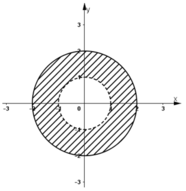

Chọn D.
Gọi ![]()
Ta có
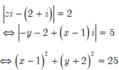
Vậy tập hợp điểm biểu diễn các số phức z là đường tròn tâm I(1;-2) và bán kính R=5

Đáp án D.
Gọi ![]()
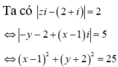
Vậy tập hợp điểm biểu diễn các số phức là đường tròn tâm I(1;-2) và bán kính R=5
Bình luận: Bài toán này ta dễ dàng nhận ra bằng phương pháp loại trừ nhất định 2 đáp án B và C đúng.
Mặt khác ![]()
Vậy biểu diễn hình học của z không thể là hình tròn:
Biểu diễn hình học của số phức.
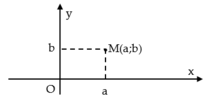
Số phức z=a+bi được biểu diễn bởi điểm M(a;b) trong mặt phẳng Oxy.

Đó là những điểm nằm phía trong hình tròn bán kính bằng 3 và phía ngoài (kể cả biên) hình tròn bán kính bằng 2 có cùng tâm là điểm biểu diễn số phức z 0 = 1 – 2i , tức là những điểm nằm trong hình vành khăn kể cả biên trong. Đó là những điểm (x; y) trên mặt phẳng tọa độ thỏa mãn điều kiện: 4 ≤ x - 1 2 + y + 2 2 < 9
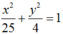
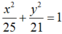


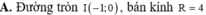

Chọn D.
Gọi M(x; y) là điểm biểu diễn số phức z = x + yi, x, y ∈ R
Gọi A là điểm biểu diễn số phức 2
Gọi B là điểm biểu diễn số phức -2
Ta có: |z – 2| + |z + 2| = 10 ⇔ MB + MA = 10.
Ta có AB = 4.
Suy ra tập hợp điểm M biểu diễn số phức z là Elip với 2 tiêu điểm là A(2; 0), B( -2; 0) tiêu cự AB = 4 = 2c, độ dài trục lớn là 10 = 2a , độ dài trục bé là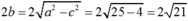
Vậy tập hợp các điểm biểu diễn các số phức z thỏa mãn điều kiện |z – 2| + |z + 2| = 10 là elip có phương trình