Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
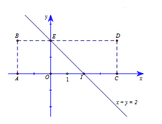
Để con châu chấu đáp xuống các điểm M x , y có x + y < 2 thì con châu chấu sẽ nhảy trong khu vực hình thang BEIA
Để M x , y có tọa độ nguyên thì x ∈ − 2 ; − 1 ; 0 ; 1 ; 2 , y ∈ 0 ; 1 ; 2
Nếu x ∈ − 2 ; − 1 thì y ∈ 0 ; 1 ; 2 ⇒ có 2.3 = 6 điểm
Nếu x = 0 thì y ∈ 0 ; 1 ⇒ có 2 điểm
Nếu x = 1 ⇒ y = 0 ⇒ có 1 điểm
có tất cả 6 + 2 + 1 = 9 điểm. Để con châu chấu nhảy trong hình chữ nhật mà đáp xuống các điểm có tọa độ nguyên thì x ∈ − 2 ; − 1 ; 0 ; 1 ; 2 ; 3 ; 4 , y ∈ 0 ; 1 ; 2 ⇒
Số các điểm M x , y có tọa độ nguyên là: 7.3 = 21 điểm. Xác suất cần tìm là: P = 9 21 = 3 7 .

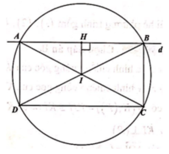
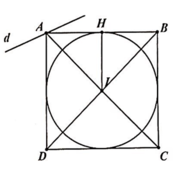
AN chính là đường thẳng AB nên AB: x-2y-2=0.
AD qua M(3/2;-3/2) và vuông góc với AB nên AD: 2x+y-3/2=0. Suy ra A(1;-1/2)
Vì M là trung điểm AD nên D(2;-5/2) suy ra BC=AD=\(\sqrt{5}\), suy ra AB=3BC=3\(\sqrt{5}\)
B(2b+2;b) nên
\(AB=\sqrt{(2b+1)^2+(b+1/2)^2}=\dfrac{\sqrt{5}}{2}|2b+1|=3\sqrt{5}\Rightarrow b=\dfrac{5}{2}\) hoặc \(b=-\dfrac{7}{2}\)
Nếu \(b=\dfrac{5}{2}\) thì B(7;5/2). Do \(\overrightarrow{BC}=\overrightarrow{AD}=(1;-2)\) nên C(8;-1/2) (thỏa mãn)
Nếu \(b=-\dfrac{7}{2}\) thì B(-5;-7/2). Do \(\overrightarrow{BC}=\overrightarrow{AD}=(1;-2)\) nên C(-4;-11/2) (loại)

Đặt BC=a, suy ra AB=3a.
$S_{MNC}=S_{ABCD}-S_{AMN}-S_{BNC}-S_{DMC}=3a^2-\dfrac{a^2}{4}-a^2-\dfrac{3a^2}{4}=a^2$
$CN=a\sqrt{5}$ nên $d(M,CN)=\dfrac{2S_{MNC}}{CN}=\dfrac{2a}{\sqrt{5}}$
Mặt khác $d(M,CN)=\dfrac{4}{\sqrt{10}}$ nên $a=\sqrt{2}$
Suy ra $MC=\dfrac{a\sqrt{37}a}{2}=\dfrac{\sqrt{74}}{2}$
Gọi C(3c+2;c) (3c+2>0) thì
$MC^2=(3c+1/2)^2+(c+3/2)^2=\dfrac{74}{4}\Leftrightarrow (6c+1)^2+(2c+3)^2=74$
$40c^2+24c-64=0$ nên c=1 hoặc c=-8/5(loại) nên C(5;1)
+ Tương tự tìm được N từ việc N thuộc CN, $MN=\dfrac{a\sqrt{5}}{2},CN=a\sqrt{5}$
+ Sau khi tìm được N ta tìm được E từ việc M là trung điểm CE
+ Tọa độ A, B xác định qua hệ thức véc tơ: vecto(EA)=3.vecto(AN); vecto(AN)=2vecto(NB)
+ Tọa độ D xác định từ việc M là trung điểm AD.

Chọn đáp án D.
Số phần tử của không gian mẫu tập hợp các điểm có tọa độ nguyên nằm trên hình chữ nhật OMNP là n(Ω)=101x11
Vì x ϵ [0;100];y ϵ [0;10] và x+y ≤90 ⇒ y = 0 → x = 0 ; 1 ; 2 ; . . . ; 90 y = 1 → x = 0 ; 1 ; 2 ; . . . ; 89 . . . y = 10 → x = 0 ; 1 ; 2 ; . . . ; 80
Khi đó có 91 + 90 + … + 81 = 946 cặp (x;y) thỏa mãn.
Vậy xác suất cần tính là P=n(X)/n(Ω)=86/101

Đáp án D.
Số phần tử của không gian mẫu tập hợp các điểm có tọa độ nguyên nằm trên hình chữ nhật OMNP là n Ω = 101 × 11.
Vì x ∈ 0 ; 100 ; y ∈ 0 ; 10 và x + y ≤ 90
⇒ y = 0 → x = 0 ; 1 ; 2 ; ... ; 90 y = 1 → x = 0 ; 1 ; 2 ; ... ; 89 ... y = 10 → x = 0 ; 1 ; 2 ; ... ; 80 .
Khi đó có 91 + 90 + ... + 81 = 946 cặp x ; y thỏa mãn.
Vậy xác suất cần tính là:
P = n ( X ) n Ω = 946 101 × 11 = 86 101 .

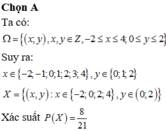

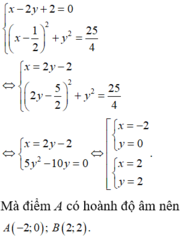

Đáp án A
Đường thẳng x + y − 2 = 0 chia hình chữ nhật thành 2 phần như hình vẽ. Xét điểm X 0 ; 1
Số các điểm nguyên không nằm bên ngoài hình chữ nhật là 3.7 = 21 (điểm)
Các điểm có tọa độ thỏa mãn x + y < 2 là các điểm nằm phía bên trái đường thẳng x + y − 2 = 0 , hay cùng phía với X so với đường thẳng x + y − 2 = 0 và không lấy các điểm nằm trên đường thẳng này.
Dễ thấy trường hợp này có 9 điểm thỏa mãn
Vậy xác suất cần tìm là 9 21 = 3 7