Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi giao điểm của CD và chiều cao của nó là E.
\(DE=\frac{24-10}{2}=7\)
Áp dụng định lý Py- ta-go vào tam giác ADE, ta được
\(AD=\sqrt{25^2-7^2}=\sqrt{576}=24\)
Vậy chiều cao của hình thang ABCD là 24cm


kẻ AE vuông góc vs DC, BF vuông góc vsDC
xét tg AED và tg BFC cò
AED =BFC=90
AD=BC ,ADE= BCF (vì tg ABCD là hthang cân)
=> tg AED =tg BFC (ch-gn)
=>DE=CF (1)
xét tg ABFE có: 3 góc vuông (tự c/m) =>tg ABFE là hcn =>AB=EF=10 cm,
ta có :DE +EF +FC =DC=24
mà EF=10cm,DE =CF => 2DE =24-10=14 =>DE=7cm
xét tg ADE vuông tại D có: AE^2 +DE^2 =AD^2
=>AE^2 +7^2 =25^2 =>AE=24cm
vậy chiều cao của hthang ABCD là 24cm

Câu 1:
Gọi mỗi đinh của tứ giác là A, B, C, D. Các góc ngoài tương ứng lần lượt là A1, B1, C1, D1
Ta có: A+ B+ C+ D+ A1+ B1+ C1+ D1= 720 độ
Ma A+ B+ C+ D= 360 độ nên A1+ B1+ C1+ D1= 720 - 360= 360 độ
Tính chiều cao của hình thang cân ABCD, biết rằng cạnh bên AD = 5cm, cạnh đáy AB = 6cm và CD = 14cm.

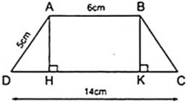
Kẻ AH ⊥ CD, BK ⊥ CD thì AH//BK nên hình thang ABKH có hai cạnh bên song song.
Áp dụng tính chất của hình thang ABKH có hai cạnh bên song song, ta có: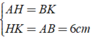
Áp dụng định lí Py – ta – go vào tam giác ADH vuông tại H ta được:
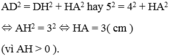
Vậy chiều cao của hình thang cân là 3cm.
Từ A,B kẻ đường cao AH,BK (H∈CD, K∈CD)
AB//HK=>ABKH là hình bình hành.
AH⊥DC=>ABKH là hình chữ nhật
=>HK=AB=10
ΔAHD= ΔBKC(ch-gn)
=>DH=HC=(DC-HK)//2=7
ΔKCB vuông tại K =>BC^2=BK^2+KC^2
=>BK=24