DT
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
2 tháng 4 2018
\(b)\) \(\left(2x-1\right)^{2012}=\left(2x-1\right)^{2010}\)
\(\Leftrightarrow\)\(\left(2x-1\right)^{2010}.\left(2x-1\right)^2=\left(2x-1\right)^{2010}\)
\(\Leftrightarrow\)\(\left(2x-1\right)^2=1\)
\(\Leftrightarrow\)\(\orbr{\begin{cases}2x-1=1\\2x-1=-1\end{cases}\Leftrightarrow\orbr{\begin{cases}2x=2\\2x=0\end{cases}}}\)
\(\Leftrightarrow\)\(\orbr{\begin{cases}x=\frac{2}{2}\\x=\frac{0}{2}\end{cases}\Leftrightarrow\orbr{\begin{cases}x=1\\x=0\end{cases}}}\)
Vậy \(x=0\) hoặc \(x=1\)
Chúc bạn học tốt ~
TD
7 tháng 7 2017
a ) \(3x\left(x-1\right)-x\left(3x-2\right)=5\)
\(\Leftrightarrow3x^2-3x-3x^2+2x=5\)
\(\Leftrightarrow-x=5\)
\(\Leftrightarrow x=-5\)
Vậy phương trình có nghiệm x = - 5 .
8 tháng 9 2023
Bạn xem lại đề nhé.
a) \(A=x^2+5y^2+2xy-4x-8y+2015\)
\(A=x^2-4x+4-2y\left(x-2\right)+y^2+2011+4y^2\)
\(A=\left(x-2\right)^2-2y\left(x-2\right)+y^2+2011+4y^2\)
\(A=\left(x-2-y\right)^2+4y^2+2011\)
Vì \(\left(x-y-2\right)^2\ge0;4y^2\ge0\)
\(\Rightarrow A_{min}=2011\)
Dấu bằng xảy ra : \(\Leftrightarrow\left\{{}\begin{matrix}x-y-2=0\\4y^2=0\end{matrix}\right.\Leftrightarrow}\left\{{}\begin{matrix}x=2\\y=0\end{matrix}\right.\)
22 tháng 7 2015
a) \(36x^2-12x-36x^2+27x=30\)
\(15x=30\)
\(x=2\)
b) \(5x-2x^2+2x^2-2x=15\)
\(3x=15\)
\(x=5\)
8 tháng 12 2019
\(5x^2+5y^2+8xy+2x-2y+2=0\)
\(\Leftrightarrow\left(x^2+2x+1\right)+\left(y^2-2y+1\right)+4\left(x^2+2xy+y^2\right)=0\)
\(\Leftrightarrow\left(x+1\right)^2+\left(y-1\right)^2+4\left(x+y\right)^2=0\)
\(\Rightarrow x=-1;y=1\)
Khi đó:
\(M=\left(1-1\right)^{2010}+\left(2-1\right)^{2011}+\left(1-1\right)^{2012}\)
\(=1\)
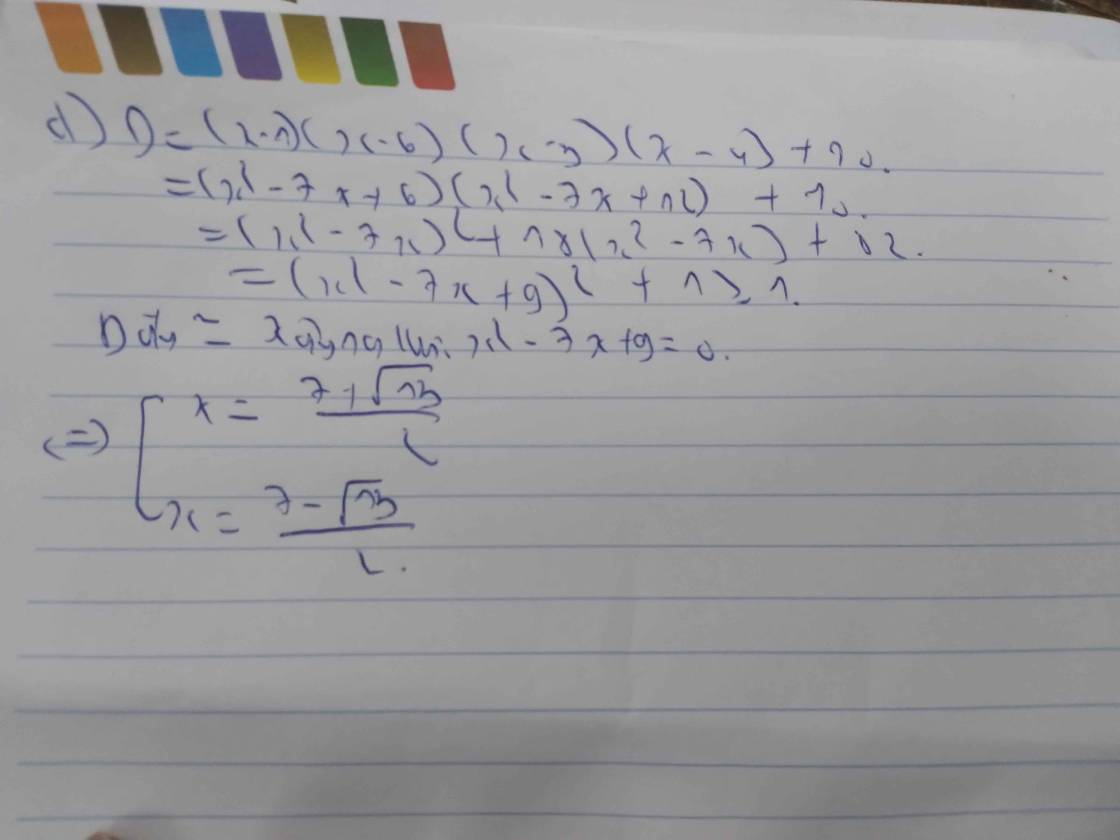
\(\left(2x-1\right)^{2012}=\left(2x-1\right)^{2010}\)
\(\Leftrightarrow\left(2x-1\right)^{2012}-\left(2x-1\right)^{2010}=0\)
\(\Leftrightarrow[\left(2x-1\right)^{2010}.\left(2x-1\right)^2]-\left(2x-1\right)^{2010}=0\)\(\Leftrightarrow\left(2x-1\right)^{2010}.[\left(2x-1\right)^2-1]=0\)
\(\Leftrightarrow\left(2x-1\right)^{2010}.[\left(2x-1-1\right)\left(2x-1+1\right)]=0\)
\(\Leftrightarrow\left(2x-1\right)^{2010}.[\left(2x-2\right)2x]=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\left(2x-1\right)^{2010}\\2x\left(2x-2\right)=0\end{matrix}\right.=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-1=0\\2x=0\\2x-2=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\\x=0\\x=1\end{matrix}\right.\)
Vậy x \(\in\left\{\dfrac{1}{2};0;1\right\}\)
\((2x-1)^{2012} = (2x-1)^{2010} \)
\(\)\(\Leftrightarrow\)\((2x-1)^{2012} - (2x-1)^{2010} = 0\)
\(\Leftrightarrow\)\((2x-1)^{2010} . [(2x-1)^{2} - 1] = 0\)
\(\Leftrightarrow\)\((2x-1)^{2010} . (2x-2).2x = 0\)
\(\Leftrightarrow\)\(4 . (2x-1)^{2010} . (x-1) . x = 0\)
\(\Rightarrow\)\(\left[{}\begin{matrix}\left(2x-1\right)^{2010}=0\\x-1=0\\x=0\end{matrix}\right.\)
\(\Rightarrow\)\(\left[{}\begin{matrix}x=\dfrac{1}{2}\\x=1\\x=0\end{matrix}\right.\)
\(Vậy \) \(x= \)\(\dfrac{1}{2}\); \(x=1\) \(hay\) \(x=0\)