
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Biến đổi về dạng (x - 3)(x + 2) = 0. Tìm được x ∈ { - 2 ; 3 }
b) Thu gọn về dạng -2x + 3 = 0. Tìm được x = 3 2

\(2x\left(2x-1\right)-\left(2x+5\right)^2=0\)
=>\(4x^2-2x-4x^2-20x-25=0\)
=>-22x-25=0
=>22x+25=0
=>22x=-25
=>\(x=-\dfrac{25}{22}\)

a. Đúng
Vì x 2 + 1 > 0 với mọi x nên phương trình đã cho tương đương với phương trình:
4x – 8 + (4 – 2x) = 0 ⇔ 2x – 4 = 0 ⇔ 2x = 4 ⇔ x = 2
b. Đúng
Vì x 2 – x + 1 = x - 1 / 2 2 + 3/4 > 0 với mọi x nên phương trình đã cho tương đương với phương trình:
(x + 2)(2x – 1) – x – 2 = 0 ⇔ (x + 2)(2x – 2) = 0
⇔ x + 2 = 0 hoặc 2x – 2 = 0 ⇔ x = - 2 hoặc x = 1
c. Sai
Vì điều kiện xác định của phương trình là x + 1 ≠ 0 ⇔ x ≠ - 1
Do vậy phương trình  không thể có nghiệm x = - 1
không thể có nghiệm x = - 1
d. Sai
Vì điều kiện xác định của phương trình là x ≠ 0
Do vậy x = 0 không phải là nghiệm của phương trình 

Ta có:
x2 + 7x + 10 = 0
<=> x^2 + 5x + 2x + 10 = 0
<=> x(x + 5) + 2(x + 5) = 0
<=> (x+2)(x+5) = 0
<=> x+2=0 hoặc x+5=0
<=> x= -2 hoặc x= -5
Vậy x = -2; -5.
\(x^2+7x+10=0\)
\(\Leftrightarrow\left(x^2+5x\right)+\left(2x+10\right)=0\)
\(\Leftrightarrow x\left(x+5\right)+2\left(x+5\right)=0\)
\(\Leftrightarrow\left(x+5\right)\left(x+2\right)=0\)
\(\Leftrightarrow\hept{\begin{cases}x+5=0\\x+2=0\end{cases}\Leftrightarrow\hept{\begin{cases}x=-5\\x=-2\end{cases}}}\)

x^2+7x+10=0
x(x+7)=-10
=>x>0 x<0
x+7<0 x+7<0
Mà x+7>x
=>x<0 =>x<0
x+7>0 x>-7
=>x thuộc -1;-2;-3;-4;-5;-6

\(3x+4=0\Leftrightarrow x=-\dfrac{4}{3}\\ 2x\left(x-1\right)-\left(1+2x\right)=-34\\ \Leftrightarrow2x^2-2x-1-2x=-34\\ \Leftrightarrow2x^2-4x+33=0\\ \Leftrightarrow2\left(x^2-2x+1\right)+30=0\\ \Leftrightarrow2\left(x-1\right)^2+30=0\\ \Leftrightarrow x\in\varnothing\left[2\left(x-1\right)^2+30\ge30>0\right]\\ x^2+9x-10=0\\ \Leftrightarrow x^2-x+10x-10=0\\ \Leftrightarrow\left(x-1\right)\left(x+10\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=1\\x=-10\end{matrix}\right.\\ \left(7x-1\right)\left(2+5x\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}7x-1=0\\2+5x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{7}\\x=-\dfrac{2}{5}\end{matrix}\right.\)

\(x^2-y^2+2x-4y-10=0\)
\(\Leftrightarrow\left(x^2+2x+1\right)-\left(y^2+4y+4\right)=7\)
\(\Leftrightarrow\left(x+1\right)^2-\left(y+2\right)^2=7\)
\(\Leftrightarrow\left(x+y+3\right)\left(x-y-1\right)=7\)
Mặt khác x,y>0 => x+y+3>x-y-1 và x+y+3>0
Nên ta có cặp nghiệm duy nhất sau: \(\hept{\begin{cases}x+y+3=7\\x-y-1=1\end{cases}\hept{\begin{cases}x+y=4\\x-y=2\end{cases}\hept{\begin{cases}x=3\\y=1\end{cases}}}}\)

Điều kiện x ≠ 2 và x ≠ 0
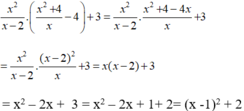
Vì x - 1 2 ≥ 0 nên x - 1 2 + 2 ≥ 2 với mọi giá trị của x.
Khi đó giá trị nhỏ nhất của biểu thức bằng 2 khi x = 1.
Vậy biểu thức đã cho có giá trị nhỏ nhất bằng 2 tại x = 1.

2x2 -x -10 =0
<=> 2x2+4x-5x-10=0
<=>2x(x+2)-5(x+2)=0
<=>(x+2)(2x-5)=0
=>\(\orbr{\begin{cases}x+2=0\\2x-5=0\end{cases}}\)<=>\(\orbr{\begin{cases}x=-2\\2x=5\end{cases}}\)<=>\(\orbr{\begin{cases}x=-2\\x=\frac{5}{2}\end{cases}}\)
vậy X =-2 hoặc x=\(\frac{5}{2}\)