HT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
18 tháng 7 2023
a. \(8x\left(x-2007\right)-2x+4034=0\)
\(\Rightarrow\left(x-2017\right)\left(4x-1\right)\)
\(\Rightarrow\left[{}\begin{matrix}x-2017=0\\4x-1=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=2017\\4x=1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2017\\x=\dfrac{1}{4}\end{matrix}\right.\)
Vậy x=2017 hoặc x=1/4
b.\(\dfrac{x}{2}+\dfrac{x^2}{8}=0\)
\(\Rightarrow\dfrac{x}{2}\left(1+\dfrac{x}{4}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{x}{2}=0\\1+\dfrac{x}{4}=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\\dfrac{x}{4}=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-4\end{matrix}\right.\)
Vậy x=0 hoặc x=-4
c.\(4-x=2\left(x-4\right)^2\)
\(\Rightarrow\left(4-x\right)-2\left(x-4\right)^2=0\)
\(\Rightarrow\left(4-x\right)\left(2x-7\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}4-x=0\\2x-7=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=4\\x=\dfrac{7}{2}\end{matrix}\right.\)
Vậy x=4 hoặc x=7/2
d.\(\left(x^2+1\right)\left(x-2\right)+2x=4\)
\(\Rightarrow\left(x-2\right)\left(x^2+3\right)=0\)
Nxet: (x2+3)>0 với mọi x
=> x-2=0 <=>x=2
Vậy x=2
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
18 tháng 7 2023
a, 8\(x\).(\(x-2007\)) - 2\(x\) + 4034 = 0
4\(x\)(\(x\) - 2007) - \(x\) + 2017 = 0
4\(x^2\) - 8028\(x\) - \(x\) + 2017 = 0
4\(x^2\) - 8029\(x\) + 2017 = 0
4(\(x^2\) - 2. \(\dfrac{8029}{8}\) \(x\) +( \(\dfrac{8029}{8}\))2) - (\(\dfrac{8029}{4}\))2 + 2017 = 0
4.(\(x\) + \(\dfrac{8029}{8}\))2 = (\(\dfrac{8029}{4}\))2 - 2017
\(\left[{}\begin{matrix}x=-\dfrac{8029}{8}+\dfrac{1}{2}.\sqrt{\left(\dfrac{8029}{4}\right)^2-2017}\\x=-\dfrac{8029}{8}-\dfrac{1}{2}.\sqrt{\left(\dfrac{8029}{4}\right)^2-2017}\end{matrix}\right.\)
TH
4
12 tháng 9 2015
=> x + 2y = 0 hoặc x2 - 2xy + 4y2 = 0
còn lại thì e bó tay . canh
12 tháng 9 2015
(x+2y)(x2-2xy+4y2)=0
<=>x3+(2y)3=0
<=>x3+8y3=0 (1)
(x-2y)(x2+2xy+4y2)=0
<=>x3-(2y)3=0
<=>x3-8y3=0 (2)
từ (1) và (2)=>x3+8y3-x3+8y3=0
<=>16y3=0
<=>y=0
thay y=0 vào (1) ta đc:
x3-0=0
<=>x3=0
<=>x=0
QN
1
26 tháng 9 2021
Ta có: \(\left(x-1\right)^2-\left(x-2\right)\left(x+2\right)=5\)
\(\Leftrightarrow x^2-2x+1-x^2+4=5\)
\(\Leftrightarrow-2x=0\)
hay x=0
NH
8 tháng 10 2017
\(A=\left(7x-1\right)^2-4\left|1-7x\right|+5\)
\(\Rightarrow MinA=5\)khi và chỉ khi x=1/7
DN
3
AH
Akai Haruma
Giáo viên
30 tháng 10 2021
Bài 1:
a. $=2x(x-3)$
b. $=x^3(x+3)+(x+3)=(x^3+1)(x+3)=(x+1)(x^2-x+1)(x+3)$
c. $=64-(x^2-2xy+y^2)=8^2-(x-y)^2$
$=(8-x+y)(8+x-y)$
AH
Akai Haruma
Giáo viên
30 tháng 10 2021
Bài 2:
$(x+5)(x+1)+(x-2)(x^2+2x+4)-x(x^2+x-2)$
$=x^2+6x+5+(x^3-2^3)-(x^3+x^2-2x)$
$=x^2+6x+5+x^3-8-x^3-x^2+2x$
$=8x-3$
Ta có đpcm.
AT
Ai giải hộ mình bài 18 với! Mình đang cần gấp lắm :(( Cảm ơn trước nha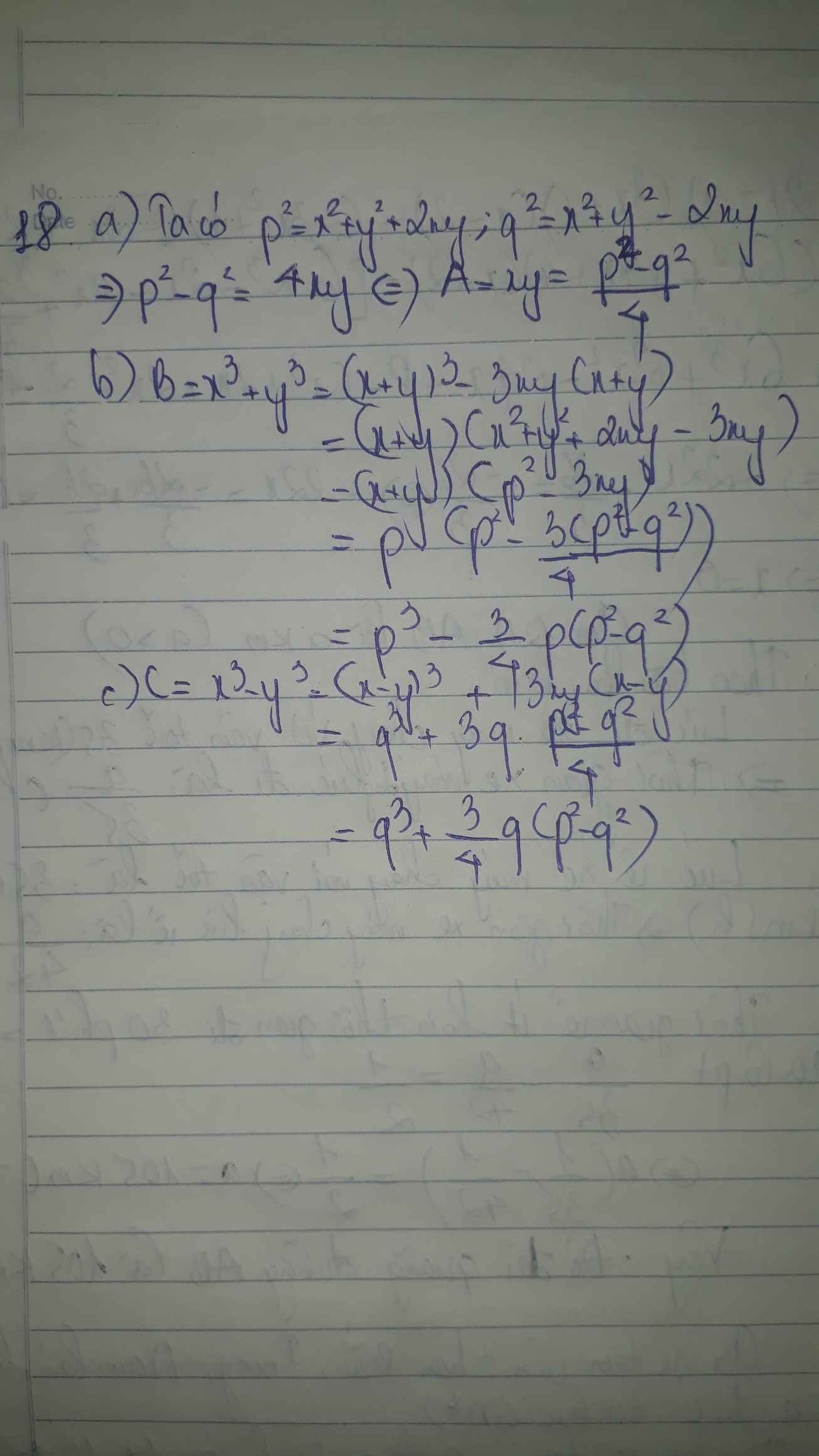
1
\(x^3-7x^2-13x+91=0\)
\(\Rightarrow x^2\left(x-7\right)-13\left(x-7\right)=0\)
\(\Rightarrow\left(x-7\right)\left(x^2-13\right)=0\)
\(\Rightarrow\left(x-7\right)\left(x-\sqrt{13}\right)\left(x+\sqrt{13}\right)=0\)
Tìm được \(x\in\left\{7;\sqrt{13};-\sqrt{13}\right\}\)