Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

`(15-x)+(x-12)=7-(-5+x)`
`=>15-x+x-12=7+5-x`
`=>3=12-x`
`=>x=12-3`
`=>x=9`
Vậy `x=9`

( 2 + x ) + ( 4 + x ) + ( 6 + x ) + ... + ( 52 + x ) = 780
( x + x + x + ... + x ) + ( 2 + 4 + 6 + ... + 52 ) = 780
26x = 780 - 702
26x = 78
x = 78 : 26
x = 3


\(\frac{2}{2.3}\) + \(\frac{2}{3.4}\) + \(\frac{2}{4.5}\) + .......+ \(\frac{2}{x.\left(x+1\right)}\) = \(\frac{2017}{2019}\)
2 . ( \(\frac{1}{2}\) - \(\frac{1}{3}\) + \(\frac{1}{3}\) - \(\frac{1}{4}\) + .......+ \(\frac{1}{x+1}\) ) = \(\frac{2017}{2019}\)
2 . ( \(\frac{1}{2}\) - \(\frac{1}{x+1}\) ) = \(\frac{2017}{2019}\)
\(\frac{1}{2}\) - \(\frac{1}{x+1}\) = \(\frac{2017}{2019}\) : 2
\(\frac{1}{2}\) - \(\frac{1}{x+1}\) = \(\frac{2017}{4038}\)
\(\frac{1}{x+1}\) = \(\frac{1}{2}\) - \(\frac{2017}{4038}\)
\(\frac{1}{x+1}\) = \(\frac{1}{2019}\)
<=> x + 1 = 2019 => x = 2018
vậy x = 2018
\(\frac{2}{2.3}+\frac{2}{3.4}+\frac{2}{4.5}+...+\frac{2}{x\left(x+1\right)}=\frac{2017}{2019}\)
\(\Leftrightarrow2\left(\frac{1}{2.3}+\frac{1}{3.4}+\frac{1}{4.5}+...+\frac{1}{x\left(x+1\right)}\right)=\frac{2017}{2019}\)
\(\Leftrightarrow2\left(\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{x}-\frac{1}{x+1}\right)=\frac{2017}{2019}\)
\(\Leftrightarrow2\left(\frac{1}{2}-\frac{1}{x+1}\right)=\frac{2017}{2019}\)
\(\Leftrightarrow\frac{1}{2}-\frac{1}{x+1}=\frac{2017}{4038}\)
\(\Leftrightarrow\frac{1}{x+1}=\frac{1}{2019}\)
\(\Rightarrow x+1=2019\)
\(\Leftrightarrow x=2018\)
Vậy \(x=2018\)

(x + 1) + (x + 2) +......+ (x + 100) = 5750
(x + x + ... + x) + (1 + 2 + 3 + ... + 100) = 5750
x . 100 + (1 + 2 + 3 + ... + 100) = 5750
x . 100 + ([1 + 100] . 100 : 2) = 5750
x . 100 + 5050 = 5750
x . 100 = 5750 - 5050
x . 100 = 700
=> x = 700 : 100 = 7

a) \(\frac{28\times7-45\times7+7\times18}{45\times14}\)
\(=\frac{7\left(28-45+7\right)}{45\times14}\)
\(=\frac{7\times\left(-10\right)}{45\times14}=\frac{-1}{9}\)
b) \(\frac{12.3-2.6}{4.5.6}\)
\(=\frac{2.6.3-2.6}{4.5.6}\)
\(=\frac{2.6\left(3-1\right)}{2.2.5.6}\)
\(=\frac{2.6.2}{2.2.5.6}\)\(=\frac{1}{5}\)

(x+1)+(x+2)+(x+3)+...+(x+100)
=(x+x+...)+(1+2+3+4+...+100)
=x.100+(1+100x100:2)
=x.100+5050=5750
x.100=5750-5050
x.100=700
x=700:100
vậy x=7
( x + 1 ) + ( x + 2 ) + ... + ( x + 100 ) = 5750
<=>( x + x + ... + x ) + ( 1 + 2 + ... + 100 ) = 5750
100 số x
<=> x.100 + ( 100 + 1 ) .100 : 2 = 5750
<=> x . 100 + 5050 = 5750
=> x . 100 = 700
=> x = 7

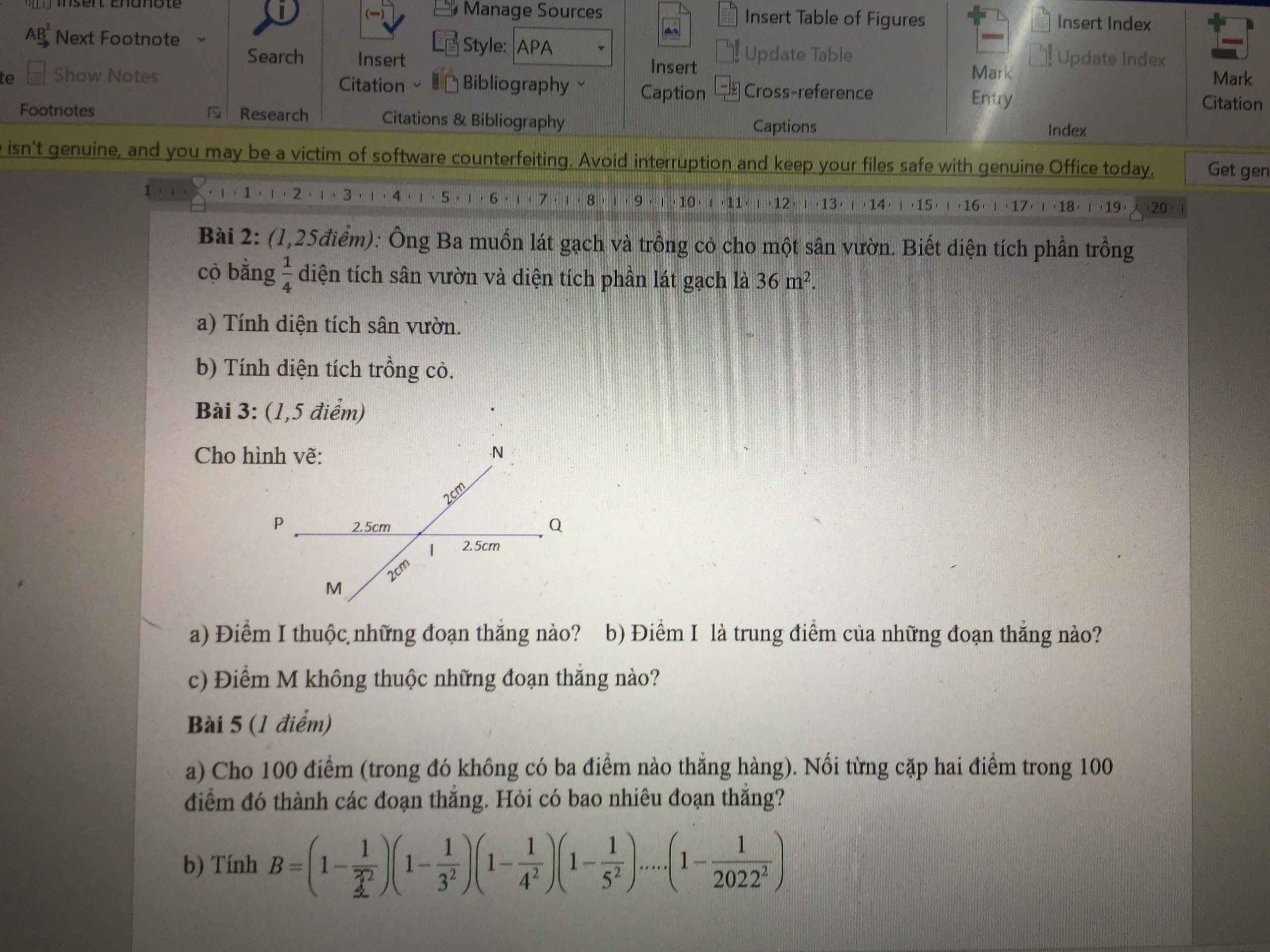
5:
a: Số đoạn thẳng tạo thành là: 100*99/2=4950(đoạn)
b: \(B=\left(1-\dfrac{1}{2}\right)\left(1-\dfrac{1}{3}\right)\cdot...\cdot\left(1-\dfrac{1}{2022}\right)\left(1+\dfrac{1}{2}\right)\cdot\left(1+\dfrac{1}{3}\right)\cdot...\cdot\left(1+\dfrac{1}{2022}\right)\)
\(=\dfrac{1}{2}\cdot\dfrac{2}{3}\cdot...\cdot\dfrac{2021}{2022}\cdot\dfrac{3}{2}\cdot\dfrac{4}{3}\cdot...\cdot\dfrac{2023}{2022}\)
=1/2022*2023/2
=2023/4044
\(\frac{2}{2.4}+\frac{2}{4.6}+....+\frac{2}{x\left(x+2\right)}=\frac{4}{9}\)
<=> \(\frac{1}{2}-\frac{1}{4}+\frac{1}{4}-\frac{1}{6}+....+\frac{1}{x}-\frac{1}{x+2}=\frac{4}{9}\)
<=> \(\frac{1}{2}-\frac{1}{x+2}=\frac{4}{9}\)
<=> \(\frac{1}{x+2}=\frac{1}{18}\)
=> \(x+2=18\)
<=> \(x=16\)
Vậy...