Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Có y ' = m 2 − m − 2 x + m 2 . Hàm số nghịch biến trên − 1 ; + ∞ ⇔ m 2 − m − 2 < 0 ⇔ m ∈ − 2 ; 1

Đáp án A.
Tập xác định: D = ℝ \ − m . Ta có y ' = m 2 − 4 x + m 2 .
Để hàm số nghịch biến trên khoảng − ∞ ; 1 thì ta phải có
m 2 − 4 < 0 1 ≤ − m ⇔ − 2 < m < 2 m ≤ − 1 ⇔ − 2 < m ≤ − 1
Lưu ý: Với cách cho đáp án như trong câu hỏi này, ta có làm như sau:
- Thử với m = − 2 . Khi đó y = − 2 x + 4 x − 2 = − 2 x − 2 x − 2 = − 2 . Suy ra với m = − 2 thì hàm số không nghịch biến trên − ∞ ; 1 . Từ đó loại được đáp án B và C.
- Thử với m = − 1 . Khi đó y = − x + 4 x − 1 . Ta có y ' = − 3 x − 1 2 < 0 ∀ x ≠ 1 .
Suy ra hàm số nghịch biến trên các khoảng − ∞ ; 1 và 1 ; + ∞ . Vậy A là đáp án đúng.

Đáp án B
Ta có y ' = 3 ( m - 1 ) + ( 2 m + 1 ) sin x để hàm số nghịch biến trên ℝ thì y ' ≤ 0 với mọi x xét BPT
3 ( m - 1 ) + ( 2 m + 1 ) sin x ≤ 0 Nếu m = - 1 2 BPT luôn đúng. Với m > - 1 2 BPT ⇔ sin x ≤ 3 ( 1 - m ) 2 m + 1 để hàm số luôn nghịch biến với mọi x thì 3 ( 1 - m ) 2 m + 1 ≥ 1 ⇒ - 1 2 < m ≤ 2 5 . Với m < - 1 2 BPT ⇔ sin x ≥ 3 ( 1 - m ) 2 m + 1 để hàm số luôn nghịch biến với mọi x thì 3 ( 1 - m ) 2 m + 1 ≤ - 1 ⇒ m < - 1 2
Kết hợp hai trường hợp ta có m ≤ 2 5

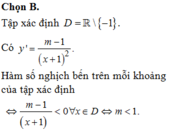
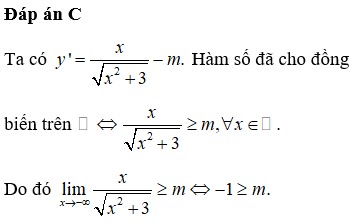
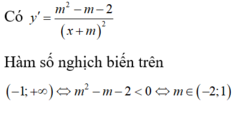


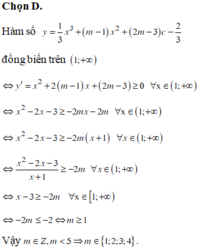
Đáp án A
Phương pháp: Để hàm số nghịch biến trên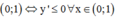 và y’ = 0 tại hữu hạn điểm.
và y’ = 0 tại hữu hạn điểm.
Cách giải: TXĐ: D =R
Hàm số nghịch biến trên khoảng (0;1) khi và chỉ khi:
TH1: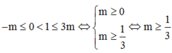
TH2: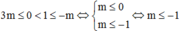
Vậy m ≥ 1 3 hoặc m ≤ - 1