K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

CM
17 tháng 11 2017
Đáp án D.
Phương pháp:
Gọi z = a + b i , sử dụng công thức tính môđun của số phức.
Cách giải:
Giả sử z = x + y i , x , y ∈ R
Theo đề bài ta có:
z + 3 − 4 i = 5 ⇔ x + 3 2 + y − 4 2 = 5 ⇔ x + 3 2 + y − 4 2 = 25
Vậy, tập hợp điểm trong mặt phẳng tọa độ biểu diễn các số phức z là đường tròn tâm I − 3 ; 4 , R = 5.


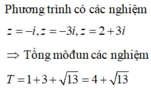






Đáp án A.
Cách 1: w = 1 + i 3 z + 2 ⇔ z = w − 2 1 + i 3 . Từ đó
z − 1 ≤ 2 ⇔ w − 2 1 + i 3 − 1 ≤ 2 ⇔ w − 3 − i 3 ≤ 2 1 + i 3 ⇔ w − 3 + i 3 ≤ 4
Vậy tập hợp cần tìm là hình tròn tâm I 3 ; 3 bán kính R = 4 . Chọn đáp án A.
Cách 2: Gọi w = x + y i ; x , y ∈ ℝ . Khi đó ta có
w = 1 + i 3 z + 2 ⇔ x + y i = 1 + i 3 z + 2 ⇔ x − 2 + y i 1 + i 3 = z
⇒ z − 1 = x − 2 + y i 1 + i 3 − 1 = x − 3 − y − 3 i 1 + i 3 ⇒ z − 1 = x − y 3 + i y − x 3 + 4 3 4
z − 1 ≤ 2 ⇒ x − y 3 2 + y − x 3 + 4 3 2 ≤ 8 ⇒ x − 3 2 + y − 3 2 ≤ 16 .
Vậy tập hợp cần tìm là hình tròn tâm I 3 ; 3 bán kính R = 4 . Chọn đáp án A.
Bài toán tổng quát: Xác định tập hợp các điểm trong mặt phẳng phức biểu diễn các số w = α z + β trong đó z là số phức tùy ý thỏa mãn z − z 0 ≤ R ( z 0 , α ≠ 0 , β là những số phức cho trước, R là số thực dương cho trước).
Tương tự như lời giải trên, ta có tập hợp cần tìm là hình tròn có tâm là điểm biểu diễn số phức α z 0 + β , với bán kính bằng R α .