Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 2:
a) Ta có: \(A=\dfrac{4}{n-1}+\dfrac{6}{n-1}-\dfrac{3}{n-1}\)
\(=\dfrac{4+6-3}{n-1}\)
\(=\dfrac{7}{n-1}\)
Để A là số tự nhiên thì \(7⋮n-1\)
\(\Leftrightarrow n-1\inƯ\left(7\right)\)
\(\Leftrightarrow n-1\in\left\{1;7\right\}\)
hay \(n\in\left\{2;8\right\}\)
Vậy: \(n\in\left\{2;8\right\}\)
ta có B=2n+9/n+2-3n+5n+1/n+2=4n+10/n+2 Để B là STN thì 4n+10⋮n+2 4n+8+2⋮n+2 4n+8⋮n+2 ⇒2⋮n+2 n+2∈Ư(2) Ư(2)={1;2} Vậy n=0

Lời giải:
a. $P=\frac{n-2}{n+5}=1-\frac{7}{n+5}$
Để $P$ nguyên thì $\frac{7}{n+5}$ nguyên.
$\Rightarrow n+5$ là ước của $7$
$\Rightarrow n+5\in\left\{\pm 1; \pm 7\right\}$
$\Rightarrow n\in\left\{-4; -6; 2; -12\right\}$
b.
Để phân số $P$ rút gọn được thì $n-2, n+5$ không nguyên tố cùng nhau.
Gọi $ƯCLN(n-2, n+5)=d$ thì $n-2\vdots d; n+5\vdots d$
$\Rightarrow 7\vdots d$
Để $n-2, n+5$ không nguyên tố cùng nhau thì $d=7$
$\Rightarrow n-2\vdots 7$
$\Rightarrow n-2=7k$ với $k$ nguyên
$\Rightarrow n=7k+2$ với $k$ là số nguyên bất kỳ.

\(a)\,\,A=\dfrac{13}{21} \Leftrightarrow \dfrac{2n+3}{4n+1}=\dfrac{13}{21} \\ \Leftrightarrow 21(2n+3)=13(4n+1)\\\Leftrightarrow 42n+63=52n+13\\\Leftrightarrow 42n-52n=13-63 \\\Leftrightarrow -10n=-50\\\Leftrightarrow n=(-50):(-10)\\\Leftrightarrow n=5\)

A = \(\dfrac{n+2}{n-1}=\dfrac{n-1+3}{n-1}=1+\dfrac{3}{n-1}\)
Để A là số nguyên thì \(3⋮n-1\)
\(\Leftrightarrow n-1\inƯ\left(3\right)\)
\(\Leftrightarrow n-1\in\left\{1;3;-1;-3\right\}\)
\(\Leftrightarrow n\in\left\{2;4;0;-2\right\}\)
có: A=\(\dfrac{n+2}{n-1}\)=\(\dfrac{n-1+3}{n-1}\)=\(1+\dfrac{3}{n-1}\)
Để A nhận giá trị nguyên thì 3/n-1 có giá trị nguyên
=> n-1ϵƯ(3)
Ta có bảng sau:
| n-1 | 1 | 3 | -1 | -3 |
| n | 2 | 4 | 0 | -2 |
Vậy nϵ\(\left\{-2;0;2;4\right\}\)

a) Ta có \(A=\dfrac{n-5}{n-3}=\dfrac{n-3-2}{n-3}=1-\dfrac{2}{n-3}\). Để \(A\inℤ\) thì \(\dfrac{2}{n-3}\inℤ\) hay \(n-3\) là ước của 2. Suy ra \(n-3\in\left\{\pm1;\pm2\right\}\).
Nếu \(n-3=1\Rightarrow n=4\); \(n-3=-1\Rightarrow n=2\); \(n-3=2\Rightarrow n=5\); \(n-3=-2\Rightarrow n=1\). Vậy để \(A\inℤ\) thì \(n\in\left\{1;2;4;5\right\}\)
\(A=\dfrac{n+4}{n+1}\) làm tương tự.
b) Dễ thấy các số ở mẫu có thể viết dưới dạng:
\(10=1+2+3+4=\dfrac{4\left(4+1\right)}{2}=\dfrac{4.5}{2}\)
\(15=1+2+3+4+5=\dfrac{5\left(5+1\right)}{2}=\dfrac{5.6}{2}\)
\(21=1+2+...+6=\dfrac{6\left(6+1\right)}{2}=\dfrac{6.7}{2}\)
...
\(120=1+2+...+15=\dfrac{15\left(15+1\right)}{2}=\dfrac{15.16}{2}\)
Do đó \(A=\dfrac{2}{4.5}+\dfrac{2}{5.6}+\dfrac{2}{6.7}+...+\dfrac{2}{15.16}\)
\(A=2\left(\dfrac{1}{4.5}+\dfrac{1}{5.6}+\dfrac{1}{6.7}+...+\dfrac{1}{15.16}\right)\)
\(A=2\left(\dfrac{5-4}{4.5}+\dfrac{6-5}{5.6}+\dfrac{7-6}{6.7}+...+\dfrac{16-15}{15.16}\right)\)
\(A=2\left(\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+...+\dfrac{1}{15}-\dfrac{1}{16}\right)\)
\(A=2\left(\dfrac{1}{4}-\dfrac{1}{16}\right)\)
\(A=\dfrac{3}{8}\)

b: =>\(\dfrac{2}{2}+\dfrac{2}{6}+\dfrac{2}{12}+...+\dfrac{2}{n\left(n+1\right)}=\dfrac{200}{101}\)
=>\(\dfrac{1}{2}+\dfrac{1}{6}+\dfrac{1}{12}+...+\dfrac{1}{n\left(n+1\right)}=\dfrac{100}{101}\)
=>1-1/2+1/2-1/3+...+1/n-1/n+1=100/101
=>1-1/(n+1)=100/101
=>1/(n+1)=1/101
=>n+1=101
=>n=100
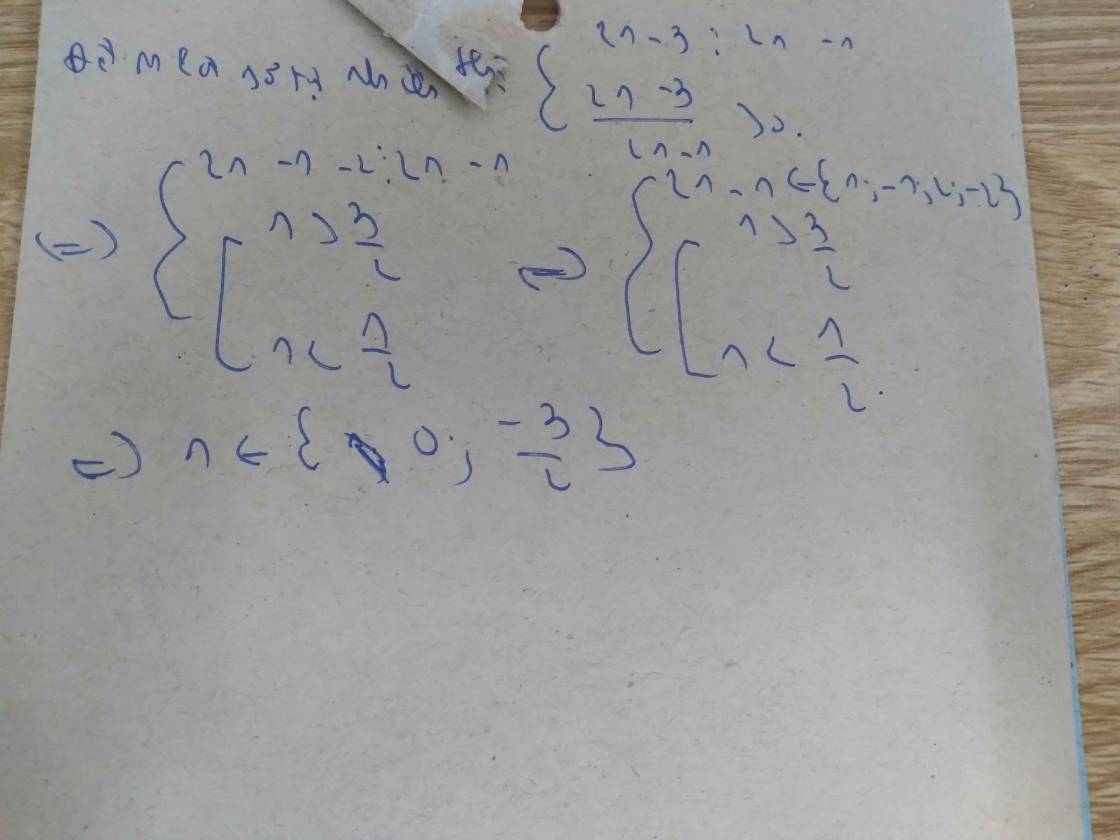
a) \(\dfrac{n+2}{3}\) là số tự nhiên khi
\(n+2⋮3\)
\(\Rightarrow n+2\in\left\{1;3\right\}\)
\(\Rightarrow n\in\left\{-1;1\right\}\left(n\in Z\right)\)
b) \(\dfrac{7}{n-1}\) là số tự nhiên khi
\(7⋮n-1\)
\(\Rightarrow7n-7\left(n-1\right)⋮n-1\)
\(\Rightarrow7n-7n+7⋮n-1\)
\(\Rightarrow7⋮n-1\)
\(\Rightarrow n-1\in\left\{1;7\right\}\Rightarrow\Rightarrow n\in\left\{2;8\right\}\left(n\in Z\right)\)
c) \(\dfrac{n+1}{n-1}\) là sô tự nhiên khi
\(n+1⋮n-1\)
\(\Rightarrow n+1-\left(n-1\right)⋮n-1\)
\(\Rightarrow n+1-n+1⋮n-1\)
\(\Rightarrow2⋮n-1\)
\(\Rightarrow n-1\in\left\{1;2\right\}\Rightarrow n\in\left\{2;3\right\}\left(n\in Z\right)\)