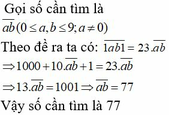Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi số cần tìm là \(\overline{ab}\), số mới là \(\overline{1ab1}\) (a,b \(\in\) N và a, b là các chữ số)
Ta có:
\(23\overline{ab}=\overline{1ab1}\)
\(\Rightarrow23\left(10a+b\right)=1000+100a+10b+1\)
\(\Rightarrow230a+23b=1001+100a+10b\)
\(\Rightarrow230a+23b-100a-10b=1001\)
\(\Rightarrow\left(230a-100a\right)+\left(23b-10b\right)=1001\)
\(\Rightarrow130a+13b=1001\)
\(\Rightarrow13\left(10a+b\right)=1001\)
\(\Rightarrow10a+b=1001:13\)
\(\Rightarrow10a+b=77\)
\(\Rightarrow10a=77-b\)
Vì \(b\le9\) nên \(68\le10a\le77\)
\(\Rightarrow10a=70\Rightarrow a=7\)
\(\Rightarrow70=77-b\)
\(\Rightarrow b=77-70=7\)
\(\Rightarrow\overline{ab}=77\)
Vậy số cần tìm là 77

gọi số cần tìm là ab
theo bài ra ta có
1ab1=abx23
1001+abx10=abx23
bớt cả 2 vế đi 10 lần ab
1001=abx13
ab=1001:13
ab=77
vậy số cần tìm là 77
tk mk nha
Gọi số cần tìm là ab
Ta có:1ab1=23ab
1000+10ab+1=23ab
1001+10ab=23ab
1001=13ab
ab=1001:13
ab=77
Vậy số duy nhất thỏa mãn đề bài là 77.

Gọi số cần tìm là ab ( a; b là chữ số )
Nếu viết thêm chữ số 1 vào bên trái và bên phải số đã cho thì ta được số mới là : 1ab1
Theo đề bài ta có :
ab . 23 = 1ab1
=> ab . 23 = 1001 + ab . 10
=> ab . 23 - ab . 10 = 1001
=> ab . (23 - 10) = 1001
=> ab . 13 = 1001
ab = 1001 : 13
ab = 77
Vậy số ban đầu cần tìm là 77.
CHÚC BẠN HỌC TỐT!!!
Gọi số cần tìm là: ab. Viết thêm 1 vào bên trái và bên phảo ta được 1ab1
Ta có: 1ab1= ab.23
1001+ ab= ab.23
=> 1001= ab.22
ab= 1001:22
ab= 45,5
Vậy số cần tìm là 45,5.

Thêm 3 quả nữa
Vì khi nếu thêm hoặc bớt đi bao nhiêu quả đi chăng nữa thi hiệu giữa hai thúng vẫn bằng là:
27 - 12 = 15 (quả cam)
Nếu số quả ở thúng thứ hai gấp đôi số quả ở thúng thứ hai thì hiệu giữa hai thúng vẫn bằng 15 quả cam.
Vậy số quả ở thúng thứ nhất là:
15 x 1 = 15( quả cam )
Vậy mỗi thúng cần phải thêm vào:
15 - 12 = 3 ( quả cam )

16:
Gọi số cần tìm là x
Theo đề, ta có: 2000+10x+2=36x
=>2002=26x
=>x=77
Bài 16: Gọi số tự nhiên cần tìm là ab.
- Theo đề bài, số tự nhiên khi thêm 2 vào bên phải và bên trái tăng gấp 36 lần, có nghĩa là: (200 + 10a + b) = 36*(100a + 10b + 2) => 8a = 35b - 7
- Vì a, b là số tự nhiên có hai chữ số nên ta thử từng giá trị của b, từ 10 đến 99. Khi b = 10, ta không tìm được giá trị nào thỏa mãn.
- Khi b = 11, ta tìm được a = 4.
- Vậy số tự nhiên cần tìm là 41.
Bài 17: Gọi số tự nhiên cần tìm là abcd.
- Theo đề bài, số tự nhiên có bốn chữ số và chữ số hàng trăm bằng 0 có nghĩa là a = 0.
- Khi xoá chữ số 0 ở hàng trăm, số đó giảm 9 lần, có nghĩa là: (1000 + 100b + 10c + d)/10 = 9*(100 + 10b + c + d) => 91b - 89c - 89d = 810
- Vì b, c, d là số tự nhiên có đến 3 chữ số nên ta thử từng giá trị của b từ 1 đến 9 và c, d từ 0 đến 9.
- Khi b = 9, ta tìm được c = 2 và d = 1. Vậy số tự nhiên cần tìm là 9021.
Bài 18: Gọi số tự nhiên cần tìm là ab.
- Theo đề bài, khi thêm một chữ số 0 vào giữa các chữ số hàng chục và hàng đơn vị của số đó, ta thu được số tự nhiên tăng gấp 9 lần.
- Số tự nhiên gốc khi đó là (a0b).
- Ta có: 10*(10a+b) = 9*(a0b) => 91a - 10b = 0 Vì a, b là số tự nhiên có hai chữ số, nên a phải bằng 1 và b = 9.
- Vậy số tự nhiên cần tìm là 109.
Bài 19: Gọi số tự nhiên cần tìm là abc.
- Số đó vừa chia hết cho 5 và chia hết cho 9, có nghĩa là tổng các chữ số của số đó chia hết cho 9.
- Ta có: a + b + c + c + b + a = 2(a + b + c) chia hết cho 9.
- Suy ra: a + b + c chia hết cho 3.
- Số đó hiệu giữa số đó với số viết theo thứ tự ngược lại bằng 297, có nghĩa là:
(100a + 10b + c) - (100c + 10b + a) = 99a - 99c = 297
=> a - c = 3 Do a + b + c chia hết cho 3 và a - c = 3, nên ta thử các cặp số thỏa mãn a + b + c = 45 và a - c = 3. Khi đó ta tìm được a = 17, b = 11, c = 17.
Vậy số tự nhiên cần tìm là 171.

Gọi số cần tìm là a b (0≤a, b≤9; a≠0)
Theo đề ra ta có: 1 a b 1 = 23 a b
=> 1000 + 10 a b + 1 = 23 a b
=> 13 a b = 1001 => a b = 77
Vậy số cần tìm là 77