
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án B.
Ta có y ' = 2 x 2 + 2 m + 1 x + m 2 + 4 m + 3 ; ∀ x ∈ ℝ .
Phương trình y ' = 0 ⇔ 2 x 2 + 2 m + 1 x + m 2 + 4 m + 3 = 0 (*).
Để hàm số đã cho có 2 điểm cực trị ⇔ (*) có 2 nghiệm phân biệt ⇔ ∆ ' > 0 ⇔ - 5 < m < - 1 .
Và các điểm cực trị của hàm số nằm bên phải Oy ⇔ m 2 + 4 m + 3 > 0 ⇔ [ m > - 1 m < - 3 .
Vậy - 5 < m < - 3 là giá trị cần tìm.

Đáp án A.
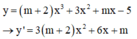
Hàm số đã cho có điểm cực đại và điểm cực tiểu đều có hoành độ dương


Hàm số có cực trị khi và chỉ khi phương trình
f ' x = m - 1 x 2 - m + 3 x + 3 - m = 0 có hai nghiệm phân biệt
Đặt x = t + 2, phương trình f ' (x) = 0 trở thành
m - 1 t 2 + 3 m - 7 t + m - 7 = 0 *
Phương trình → có hai nghiệm x 1 , x 2 thỏa x 1 < 2 < x 2 khi và chỉ khi phương trình (*) có hai nghiệm trái dấu m - 7 m - 1 < 0 ⇔ 1 < m < 7
Đáp án C

y ' = x 2 - 2 m x + m 2 - 1
Dễ thấy rằng hàm số có hai điểm cực trị x = m + 1; x = m - 1 với mọi m
Ta có:
y C D + y C T > 2 ⇔ y m + 1 + y m - 1 > 2 ⇔ 2 m 3 - 2 m + 2 > 2 ⇔ - 1 < m < 0 m > 1
Đáp án A

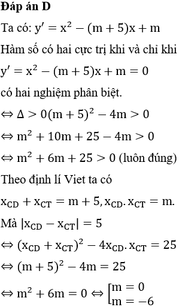
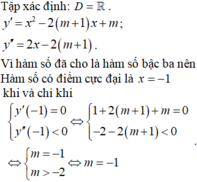


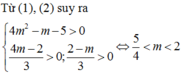
bước 1: ta tính y'
bước 2: giải pt y'=0 tìm ra xi
bước 3 tính y''
để hàm số có cực đại thì y''(xi)<0
đểhàm số có cực tiểu thì y''(xi)>0
giả các pt ta tìm đc điều kiện của m hàm số có cực đại, cực tiểu