Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(P=\sqrt[]{x}+\dfrac{3}{\sqrt[]{x}-1}\left(x>1\right)\)
\(P=\sqrt[]{x}-1+\dfrac{3}{\sqrt[]{x}-1}+1\)
Áp dụng bất đẳng thức Cauchy cho 2 số \(\sqrt[]{x}-1;\dfrac{3}{\sqrt[]{x}-1}\) ta được :
\(\sqrt[]{x}-1+\dfrac{3}{\sqrt[]{x}-1}\ge2\sqrt[]{\sqrt[]{x}-1.\dfrac{3}{\sqrt[]{x}-1}}\)
\(\Rightarrow\sqrt[]{x}-1+\dfrac{3}{\sqrt[]{x}-1}\ge2\sqrt[]{3}\)
\(\Rightarrow P=\sqrt[]{x}-1+\dfrac{3}{\sqrt[]{x}-1}+1\ge2\sqrt[]{3}+1\)
\(\Rightarrow Min\left(P\right)=2\sqrt[]{3}+1\)

ĐKXĐ : \(x>0\)
Áp dụng bất đẳng thức Cauchy cho 2 số dương \(\sqrt{x};\dfrac{4}{\sqrt{x}}\) ta có
\(P=\sqrt{x}+\dfrac{4}{\sqrt{x}}\ge2\sqrt{\sqrt{x}.\dfrac{4}{\sqrt{x}}}=4\)
Dấu "=" xảy ra khi \(\sqrt{x}=\dfrac{4}{\sqrt{x}}\Leftrightarrow x=4\)
\(P=\sqrt[]{x}+\dfrac{4}{\sqrt[]{x}}\left(x>0\right)\)
\(P=\dfrac{x+4}{\sqrt[]{x}}=\dfrac{x+4}{\sqrt[]{x}}\)
Vì \(x>0;x+4>4\)
\(\Rightarrow P=\dfrac{x+4}{\sqrt[]{x}}>4\)
⇒ Không có giá trị nhỏ nhất

\(T=\dfrac{\sqrt{27}+3}{\sqrt{3}}=\dfrac{3\sqrt{3}+3}{\sqrt{3}}=\dfrac{3\left(\sqrt{3}+1\right)}{\sqrt{3}}=\sqrt{3}\left(\sqrt{3}+1\right)=3+\sqrt{3}\)
Dạ √27 + 3 / √3 ạ 3 với căn 3 là chung với nhau ý ạ chứ ko phải như trên ý ạ

Lần sau tìm nơi gõ công thức và gõ hẳn ra nhé e <3
Áp dụng BĐT Cauchy-Schwarz ta có:
\(P=x^4+y^4\ge\frac{\left(x^2+y^2\right)^2}{2}\ge\frac{\left(\frac{\left(x+y\right)^2}{2}\right)^2}{2}=\frac{\left(\frac{2^2}{2}\right)^2}{2}=...\text{(tự tính nhé :)}\)
Khi \(x=y=1\)

Lời giải:
Để $\sqrt{x^2+3}$ có nghĩa thì $x^2+3\geq 0$
Điều này luôn đúng với mọi $x\in\mathbb{R}$ do $x^2\geq 0, \forall x\in\mathbb{R}\Rightarrow x^2+3>0, \forall x\in\mathbb{R}$
Vậy đkxđ là $x\in\mathbb{R}$

\(A=\dfrac{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}{x-\sqrt{x}+1}-\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}{\sqrt{x}+2}\\ A=\sqrt{x}+1-\sqrt{x}+2=3\)
Anh có thể giải từng bước giúp e ko ạ e ch hỉu lắm í ạ em cảm ơn

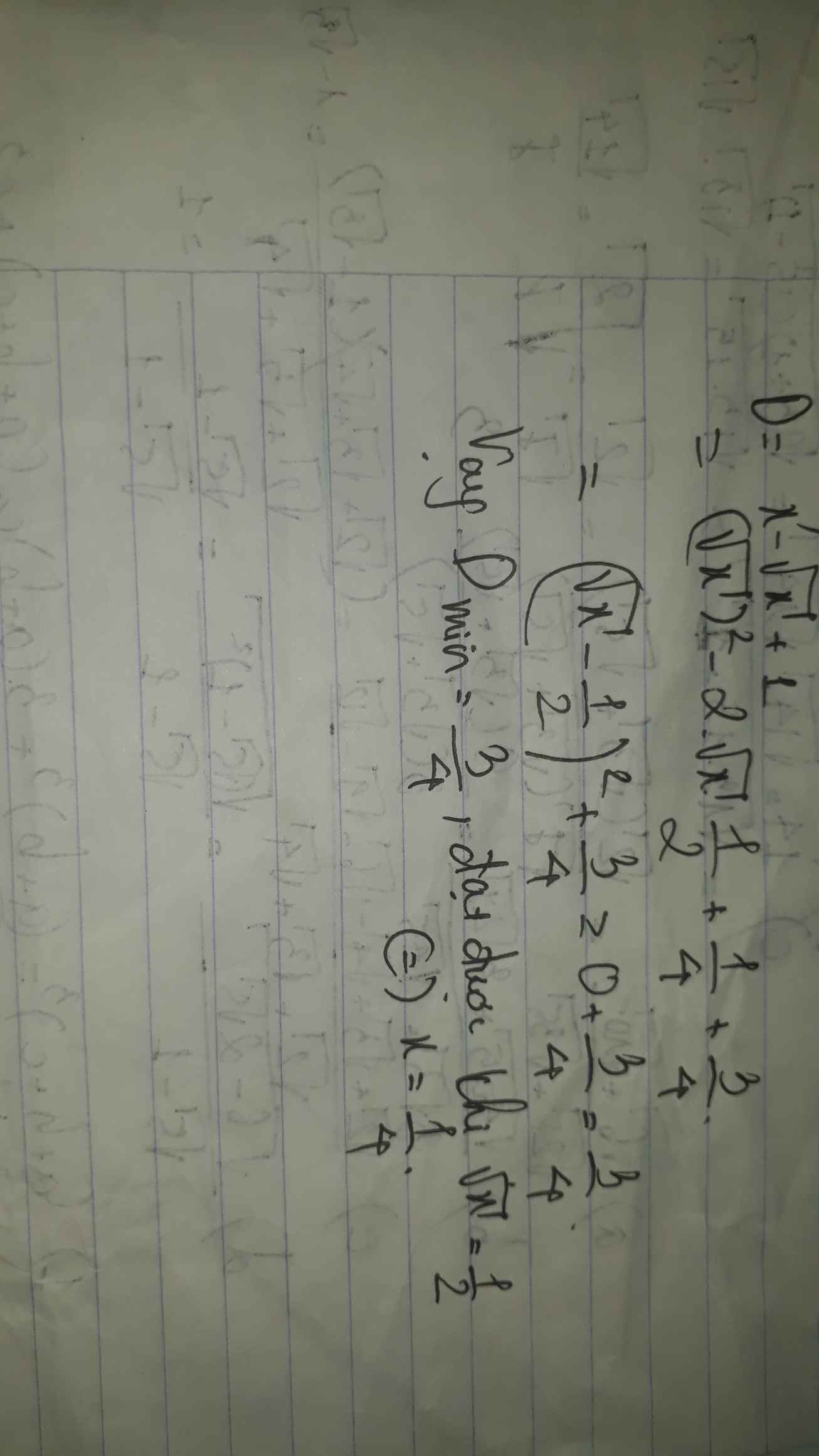


\(P=\dfrac{x+5}{\sqrt[]{x}+2}=\dfrac{x-4+9}{\sqrt[]{x}+2}=\dfrac{\left(\sqrt[]{x}+2\right)\left(\sqrt[]{x}-2\right)+9}{\sqrt[]{x}+2}\)
\(=\left(\sqrt[]{x}-2\right)+\dfrac{9}{\sqrt[]{x}+2}=\left(\sqrt[]{x}+2\right)+\dfrac{9}{\sqrt[]{x}+2}-4\)
Áp dụng bất đẳng thức Cauchy cho 2 số \(\left(\sqrt[]{x}+2\right);\dfrac{9}{\sqrt[]{x}+2}\left(x\ge0\right)\)
\(\left(\sqrt[]{x}+2\right)+\dfrac{9}{\sqrt[]{x}+2}\ge2\sqrt[]{\left(\sqrt[]{x}+2\right).\dfrac{9}{\sqrt[]{x}+2}}=2.3=6\)
\(\Rightarrow P=\left(\sqrt[]{x}+2\right)+\dfrac{9}{\sqrt[]{x}+2}-4\ge6-4=2\)
\(\Rightarrow P\ge2\Rightarrow Min\left(P\right)=2\)
Bạn xem lại đề có phải \(P=x+\dfrac{5}{\sqrt[]{x}+2}\) không?