
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Ta có: \(P\left(x\right)=7x^3+3x^4-x^2+5x^2-6x^3-2x^4+2017-x^3\)
\(=x^4+4x^2+2017\)
b) Bậc của P(x) là 4
c) Các hệ số của P(x) là 1;4;2017
Hệ số cao nhất là 4
Hệ số tự do là 2017
d) \(P\left(0\right)=0^4+4\cdot0^2+2017=2017\)
\(P\left(1\right)=1^4+4\cdot1^2+2017=1+4+2017=2022\)
\(P\left(-1\right)=\left(-1\right)^4+4\cdot\left(-1\right)^2+2017=1+4+2017=2022\)
e) \(P\left(-a\right)=\left(-a\right)^4+4\cdot\left(-a\right)^2+2017=a^4+4a^2+2017\)
\(P\left(a\right)=a^4+4a^2+2017\)
Do đó: P(-a)=P(a)

GIÚP MIK VS NHA:(((((
CẢM ƠN RẤT NHIỀU
MN XONG CÂU NÀO THÌ CỨ GỬI LUÔN CHO MIK CÂU ĐÓ NHA;-;
MIK CÒN CHÉP KỊP
:(((((((((((((( NHANHH NHANH GIÚP MIK Ạ
Câu 1:
\(a,\dfrac{x}{4}=\dfrac{y}{7}=\dfrac{x-y}{4-7}=\dfrac{-15}{-3}=5\\ \Rightarrow\left\{{}\begin{matrix}x=20\\y=35\end{matrix}\right.\\ b,\dfrac{x}{3}=\dfrac{y}{5}=\dfrac{x+y}{3+5}=\dfrac{-32}{8}=-4\\ \Rightarrow\left\{{}\begin{matrix}x=-12\\y=-20\end{matrix}\right.\\ c,\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{5}=\dfrac{x+y+z}{2+3+5}=\dfrac{-90}{10}=-9\\ \Rightarrow\left\{{}\begin{matrix}x=-18\\y=-27\\z=-45\end{matrix}\right.\\ d,\dfrac{x}{4}=\dfrac{y}{2}=\dfrac{z}{7}=\dfrac{2x-4y+3z}{8-8+21}=\dfrac{42}{21}=2\\ \Rightarrow\left\{{}\begin{matrix}x=8\\y=4\\z=14\end{matrix}\right.\)
\(e,\dfrac{x}{5}=\dfrac{y}{6}=\dfrac{z}{7}=\dfrac{z-x}{7-5}=\dfrac{30}{2}=15\\ \Rightarrow\left\{{}\begin{matrix}x=75\\y=90\\z=105\end{matrix}\right.\\ f,\Rightarrow\dfrac{x}{3}=\dfrac{y}{5};\dfrac{x}{4}=\dfrac{z}{3}\Rightarrow\dfrac{x}{12}=\dfrac{y}{20}=\dfrac{z}{9}=\dfrac{x-y-z}{12-20-9}=\dfrac{-68}{-17}=4\\ \Rightarrow\left\{{}\begin{matrix}x=48\\y=80\\z=36\end{matrix}\right.\\ g,\Rightarrow\dfrac{x}{6}=\dfrac{y}{4}=\dfrac{z}{3}=\dfrac{x+y+z}{6+4+3}=\dfrac{65}{13}=5\\ \Rightarrow\left\{{}\begin{matrix}x=30\\y=20\\z=15\end{matrix}\right.\\ h,\Rightarrow\dfrac{x}{4}=\dfrac{y}{6};\dfrac{y}{5}=\dfrac{z}{8}\Rightarrow\dfrac{x}{20}=\dfrac{y}{30}=\dfrac{z}{48}=\dfrac{5x-3y-3z}{100-90-144}=\dfrac{-536}{-134}=4\\ \Rightarrow\left\{{}\begin{matrix}x=80\\y=120\\z=192\end{matrix}\right.\)

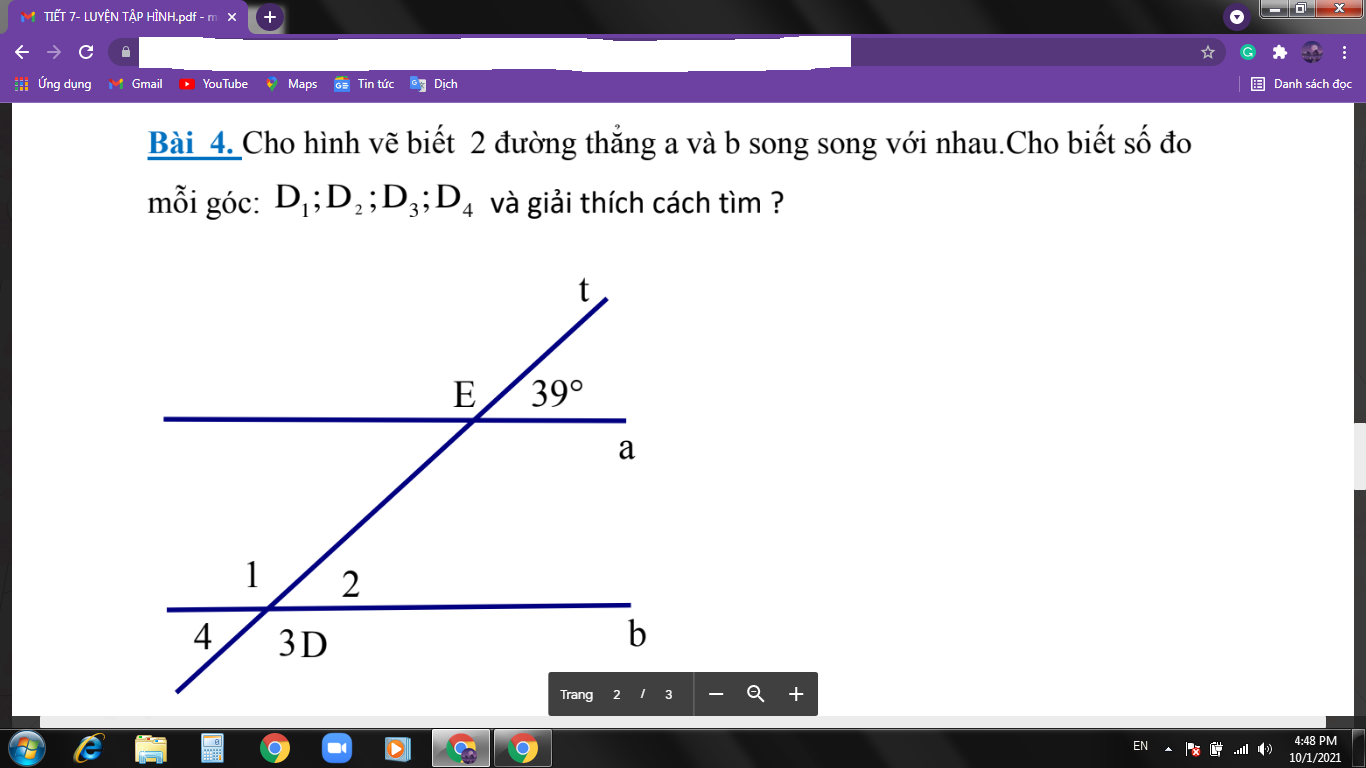
góc tEa = góc D2 =390 ( so le trong do a//b)
góc D1 = 180 0 - góc D2 ( do góc D1 + góc D2 =1800)
= 1800-390=1410
góc D3 = góc D1 = 1410 ( đối đỉnh )
góc D4 = góc D2 = 390(đối đỉnh)


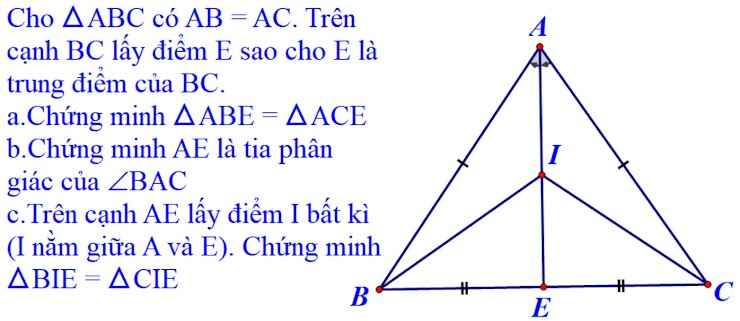
a) Xét tam giác ABE và tam giác ACE có:
+ AE chung.
+ AB = AC (gt).
+ BE = CE (E là trung điểm của BC).
=> Tam giác ABE = Tam giác ACE (c - c - c).
b) Xét tam giác ABC có: AB = AC (gt).
=> Tam giác ABC cân tại A.
Mà AE là đường trung tuyến (E là trung điểm của BC).
=> AE là phân giác ^BAC (Tính chất các đường trong tam giác cân).
c) Xét tam giác ABC cân tại A có:
AE là phân giác ^BAC (cmt).
=> AE là đường cao (Tính chất các đường trong tam giác cân).
=> AE \(\perp\) BC.
Xét tam giác BIE và tam giác CIE:
+ IE chung.
+ BE = CE (E là trung điểm của BC).
+ ^BEI = ^CEI ( = 90o).
=> Tam giác BIE = Tam giác CIE (c - g - c).

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x-1}{2}=\dfrac{y+3}{4}=\dfrac{z-5}{6}=\dfrac{-3x-4y+5z+3-12-25}{-3\cdot2-4\cdot4+5\cdot6}=\dfrac{16}{8}=2\)
Do đó: x=5; y=5; z=17

\(\dfrac{3a-2b}{5}=\dfrac{2c-5a}{3}=\dfrac{5b-3c}{2}=\dfrac{6c-15a}{9}=\dfrac{10b-6c}{4}=\dfrac{6c-15a+10b-6c}{9+4}=\dfrac{10b-15a}{13}\)
\(\Rightarrow\dfrac{3a-2b}{5}=\dfrac{10b-15a}{13}\Rightarrow39a-26b=50b-75a\)
\(\Rightarrow114a=76b\Rightarrow b=\dfrac{3}{2}a\)
Tương tự:
\(\dfrac{2c-5a}{3}=\dfrac{3a-2b}{5}=\dfrac{5b-3c}{2}=\dfrac{15a-10b}{25}=\dfrac{10b-6c}{4}=\dfrac{15a-10b+10b-6c}{25+4}=\dfrac{15a-6c}{29}\)
\(\Rightarrow\dfrac{2c-5a}{3}=\dfrac{15a-6c}{29}\Rightarrow58c-145a=45a-18c\)
\(\Rightarrow76c=190a\Rightarrow c=\dfrac{5}{2}a\)
Thế vào \(a^2+275=bc\)
\(\Rightarrow a^2+275=\left(\dfrac{3}{2}a\right).\left(\dfrac{5}{2}a\right)=\dfrac{15}{4}a^2\)
\(\Rightarrow\dfrac{11}{4}a^2=275\Rightarrow a^2=100\Rightarrow a=\pm10\)
- Với \(a=10\Rightarrow b=\dfrac{3}{2}a=15\) ; \(c=\dfrac{5}{2}a=25\)
- Với \(a=-10\Rightarrow b=-15;c=-25\)

a) Xét ∆AHB(<H=90°(gt)) và ∆AHC(<H=90°(gt)), ta có:
AB=AC(gt)
<B=<C(gt)
⟹∆AHB=∆AHC(c.h-g.n)
b) Xét ∆AHM(<M=90°(gt)) và ∆AHN(<N=90°(gt)), ta có:
AH cạnh chung
<MAH=NAH( vì ∆AHB=∆AHC(CM ở a))
⟹∆AHM=∆AHN(c.h-g.n)
⟹AM=AN ( 2 cạnh tương ứng)
⟹∆AMN cân tại A
c)Ta có: <M=<N=(180°-<A)/2
<B=<C=(180°-<A)/2
⟹ <M=<N=<B=<C
⟹<M=<B mà 2 góc này lại ở vị trí đồng vị
⟹MN//BC
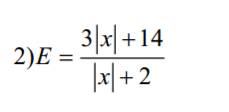 tìm gtln. tối nay mik phải nộp r, pls
tìm gtln. tối nay mik phải nộp r, pls

 giúp mik với tối nay phải nộp rồi
giúp mik với tối nay phải nộp rồi

Lời giải:
\(E=\frac{3(|x|+2)+8}{|x|+2}=3+\frac{8}{|x|+2}\)
Vì $|x|\geq 0$ với mọi $x$ nên $|x|+2\geq 2$
$\Rightarrow \frac{8}{|x|+2}\leq 4$
$\Rightarrow E=3+\frac{8}{|x|+2}\leq 3+4=7$
Vậy $E_{\max}=7$. Giá trị này đạt tại $x=0$