
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



c: \(-10-\left(\dfrac{-2017}{2021}\right)^0+\left(\dfrac{1}{5}\right)^2:\dfrac{-1}{5}-\left|0.8\right|\)
\(=-11+\dfrac{1}{5^2}\cdot\dfrac{-5}{1}-\dfrac{4}{5}\)
\(=-11+\dfrac{-1}{5}-\dfrac{4}{5}\)
=-11-1
=-12

a) Xét ∆AHB(<H=90°(gt)) và ∆AHC(<H=90°(gt)), ta có:
AB=AC(gt)
<B=<C(gt)
⟹∆AHB=∆AHC(c.h-g.n)
b) Xét ∆AHM(<M=90°(gt)) và ∆AHN(<N=90°(gt)), ta có:
AH cạnh chung
<MAH=NAH( vì ∆AHB=∆AHC(CM ở a))
⟹∆AHM=∆AHN(c.h-g.n)
⟹AM=AN ( 2 cạnh tương ứng)
⟹∆AMN cân tại A
c)Ta có: <M=<N=(180°-<A)/2
<B=<C=(180°-<A)/2
⟹ <M=<N=<B=<C
⟹<M=<B mà 2 góc này lại ở vị trí đồng vị
⟹MN//BC

Do \(\overline{2x9y1}\) là số chính phương \(\Rightarrow\overline{2x9y1}=k^2\)
\(\overline{2x9y1}\) có tận cùng bằng 1 \(\Rightarrow k\) tận cùng bằng 1 hoặc 9
Mặt khác \(20164< \overline{2x9y1}< 30276\Rightarrow142^2< \overline{2x9y1}< 174^2\)
\(\Rightarrow142^2< k^2< 174^2\)
\(\Rightarrow142< k< 174\)
Do k có tận cùng bằng 1 hoặc 9 \(\Rightarrow\) k chỉ có thể là 1 trong các số: 149, 151, 159, 161, 169, 171
Kiểm tra ta thấy chỉ có \(k=161\Rightarrow k^2=25921\) là có dạng thỏa mãn \(\overline{2x9y1}\)
Vậy \(\left\{{}\begin{matrix}x=5\\y=2\end{matrix}\right.\)

Câu hỏi của le ngoc han - Toán lớp 7 - Học toán với OnlineMath

Bài 1:
1) Kẻ tia Cx//AB//DE
Ta có: Cx//AB
\(\Rightarrow\widehat{BAC}+\widehat{ACx}=180^0\)(2 góc trong cùng phía)
\(\Rightarrow\widehat{ACx}=180^0-\widehat{BAC}=180^0-140^0=40^0\)
Ta có: Cx//DE
\(\Rightarrow\widehat{xCD}+\widehat{CDE}=180^0\)( 2 góc trong cùng phía)
\(\Rightarrow\widehat{xCD}=180^0-\widehat{CDE}=180^0-150^0=30^0\)
\(\Rightarrow\widehat{ACD}=\widehat{ACx}+\widehat{xCD}=40^0+30^0=70^0\)
2) Ta có AB//DE(gt)
Mà DE⊥MN
=> AB⊥MN =>\(\widehat{AMN}=90^0\Rightarrow\dfrac{1}{2}\widehat{AMN}=45^0\Rightarrow\widehat{AMP}=45^0\) (do MP là tia phân giác \(\widehat{AMN}\))
Ta có AB//DE
=> \(\widehat{AMP}+\widehat{DPM}=180^0\) (2 góc trong cùng phía)
\(\Rightarrow\widehat{DPM}=180^0-\widehat{AMP}=180^0-45^0=135^0\)

a) Ta có: \(P\left(x\right)=7x^3+3x^4-x^2+5x^2-6x^3-2x^4+2017-x^3\)
\(=x^4+4x^2+2017\)
b) Bậc của P(x) là 4
c) Các hệ số của P(x) là 1;4;2017
Hệ số cao nhất là 4
Hệ số tự do là 2017
d) \(P\left(0\right)=0^4+4\cdot0^2+2017=2017\)
\(P\left(1\right)=1^4+4\cdot1^2+2017=1+4+2017=2022\)
\(P\left(-1\right)=\left(-1\right)^4+4\cdot\left(-1\right)^2+2017=1+4+2017=2022\)
e) \(P\left(-a\right)=\left(-a\right)^4+4\cdot\left(-a\right)^2+2017=a^4+4a^2+2017\)
\(P\left(a\right)=a^4+4a^2+2017\)
Do đó: P(-a)=P(a)

Lời giải:
\(E=\frac{3(|x|+2)+8}{|x|+2}=3+\frac{8}{|x|+2}\)
Vì $|x|\geq 0$ với mọi $x$ nên $|x|+2\geq 2$
$\Rightarrow \frac{8}{|x|+2}\leq 4$
$\Rightarrow E=3+\frac{8}{|x|+2}\leq 3+4=7$
Vậy $E_{\max}=7$. Giá trị này đạt tại $x=0$
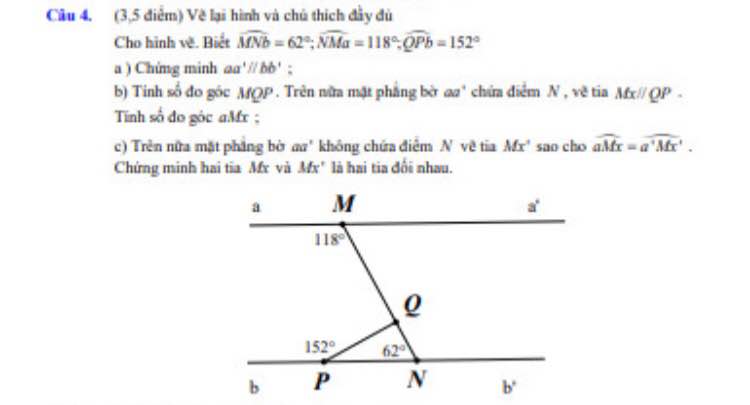
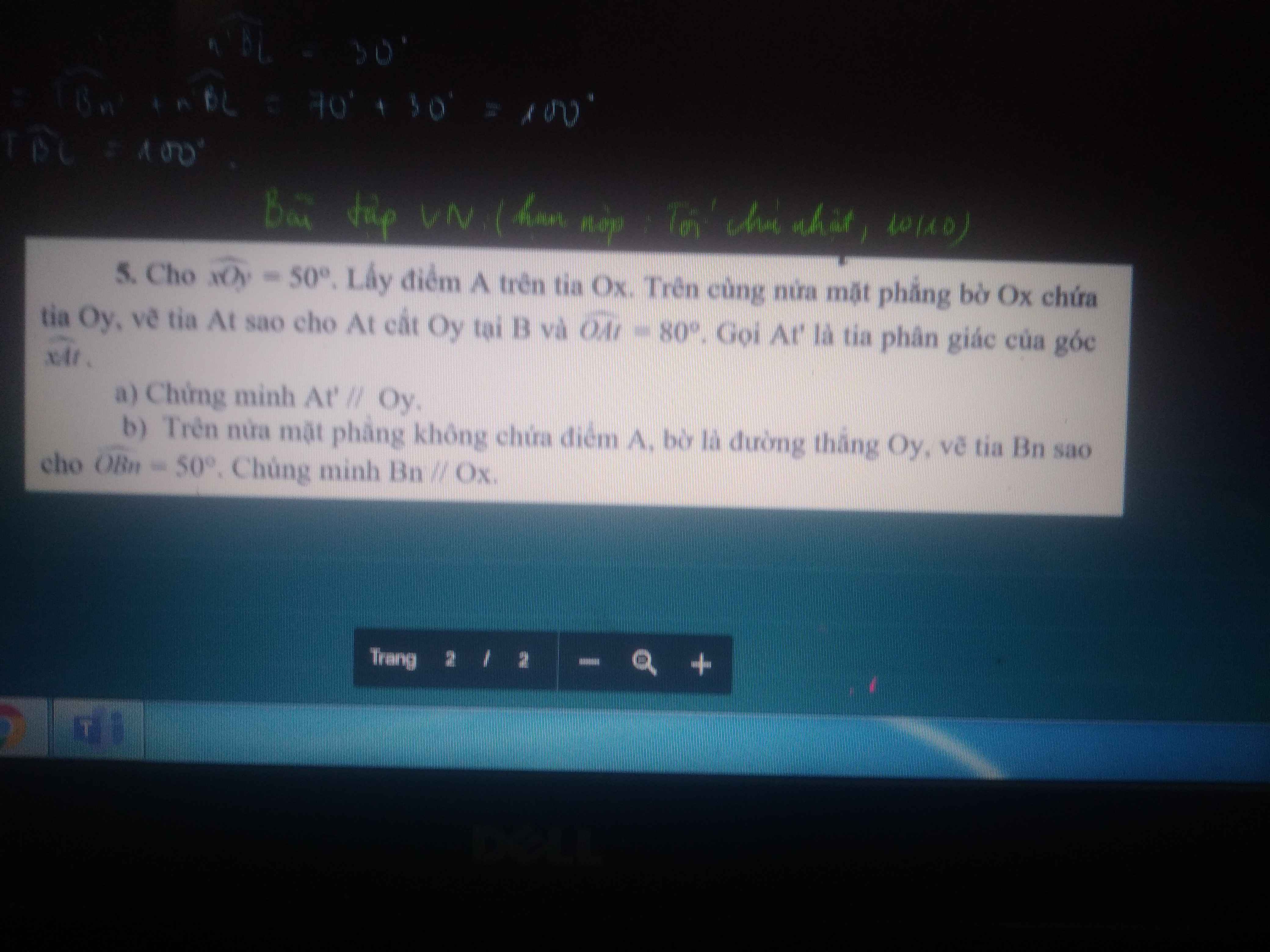
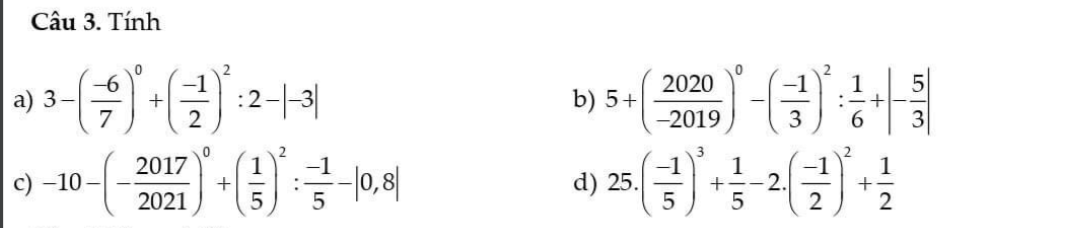


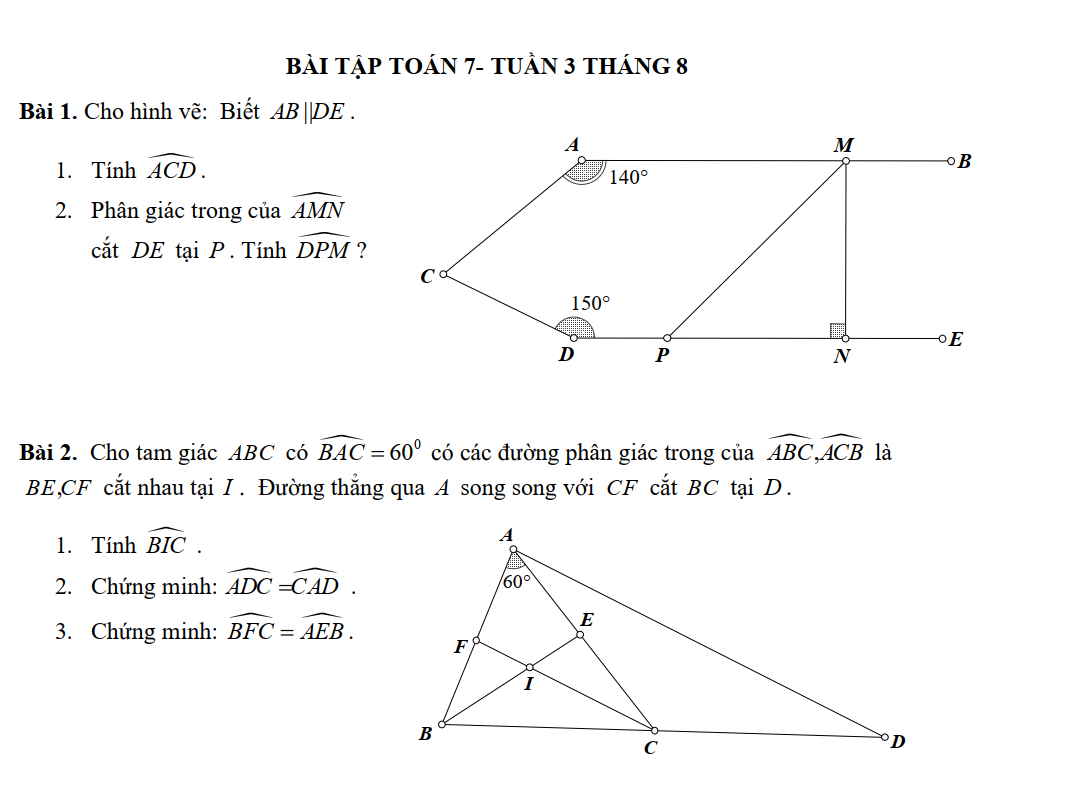

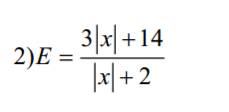 tìm gtln. tối nay mik phải nộp r, pls
tìm gtln. tối nay mik phải nộp r, pls