K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
21 tháng 10 2021
a: \(\cos\alpha=\dfrac{1}{2}\)
\(\tan\alpha=\sqrt{3}\)
\(\cot\alpha=\dfrac{\sqrt{3}}{3}\)
CM
27 tháng 1 2019
a)
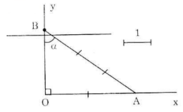
Vẽ góc vuông xOy. Trên tia Ox, lấy điểm A sao cho OA = 2cm. Lấy A làm tâm, vẽ cung tròn bán kính 3cm sao cho cung tròn này cắt tia Oy tại B. Khi đó ∠OBA = α.
Thật vậy:
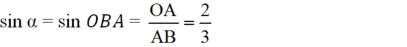
b)
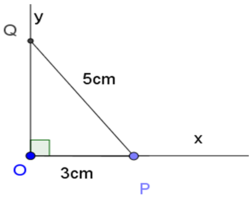
Vẽ góc vuông xOy. Trên tia Ox lấy điểm P sao cho OP = 3cm. Lấy P làm tâm, vẽ cung tròn bán kính 5cm sao cho cung này cắt tia Oy tại Q. Khi đó ∠OPQ = α.
Thật vậy:
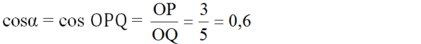
c)
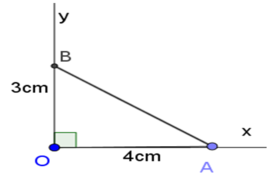
Vẽ góc vuông xOy. Trên tia Ox lấy điểm A sao cho OA = 4(cm). Trên tia Oy lấy điểm B sao cho OB = 3cm. Khi đó ∠OAB = α.
Thật vậy:
d)
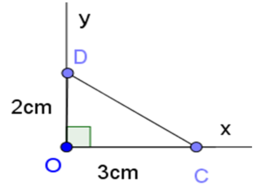
Vẽ góc vuông xOy. Trên tia Ox lấy điểm C sao cho OC = 3cm. Trên tia Oy lấy D sao cho OD = 2cm. Khi đó OCD = α.
Thật vậy:
PT
1
CM
21 tháng 6 2017
Vì α là góc nhọn nên ta có sinα > 0.
Ta lại có: sin 2 α + cos 2 α = 1
PT
1
PT
1
CM
11 tháng 2 2017
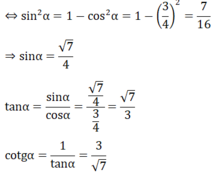
Dựng một tam giác vuông ta có:
a, Độ dài cạnh góc vuông là 3, cạnh huyền là 5, góc đối diện với cạnh góc vuông đó là góc α
b, Độ dài cạnh góc vuông là 4, cạnh huyền là 7,góc giữa cạnh góc vuông và cạnh huyền đó là góc α
c, Độ dài hai cạnh góc vuông là 3 và 2, góc đối diện với cạnh góc vuông độ dài 3 là góc α
d, Độ dài hai cạnh góc vuông là 5 và 6, góc đối diện với cạnh góc vuông độ dài 6 là góc α
H
23 tháng 8 2023
b)
Có: \(cot\alpha=\dfrac{cos\alpha}{sin\alpha}\)
Vì $\alpha $ là góc nhọn nên `0<sin\alpha<1`
\(\Rightarrow\dfrac{cos\alpha}{sin\alpha}>\dfrac{cos\alpha}{1}=cos\alpha\)
Vậy \(cos\alpha< cot\alpha\)
PT
1
CM
23 tháng 7 2017
Cho α là góc nhọn, sinα = 1/2. Tính cosα; tanα; cotα
Ta có: sin 2 α + cos 2 α = 1
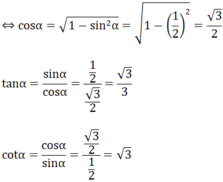
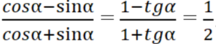
`sin α=cos α`
`<=> sinα : cosα = cosα : cosα`
`<=> tanα=1`
`<=>α=45^o`
Lời giải:
Xét tam giác $ABC$ vuông tại $A$ có $\widehat{B}=\alpha$
$\cos \alpha = \frac{AB}{BC}$
$\sin \alpha = \frac{AC}{BC}$
$\cos \alpha = \sin \alpha \Leftrightarrow AB=AC\Leftrightarrow ABC$ là tam giác vuông cân
$\Leftrightarrow \widehat{B}=\widehat{C}=45^0$
Vậy $\alpha = 45^0$