Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Tìm được sinα = 24 5 , tanα = 24 , cotα = 1 24
b, cosα = 5 3 , tanα = 2 5 , cotα = 5 2
c, sinα = ± 2 5 , cosα = ± 1 5 , cotα = 1 2
d, sinα = ± 1 10 , cosα = ± 3 10 , tanα = 1 3

Cho α là góc nhọn, sinα = 1/2. Tính cosα; tanα; cotα
Ta có: sin 2 α + cos 2 α = 1
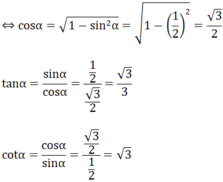

Bài 3:
Ta có: \(A=\cos^220^0+\cos^240^0+\cos^250^0+\cos^270^0\)
\(=\left(\sin^270^0+\cos^270^0\right)+\left(\sin^250^0+\cos^250^0\right)\)
=1+1
=2

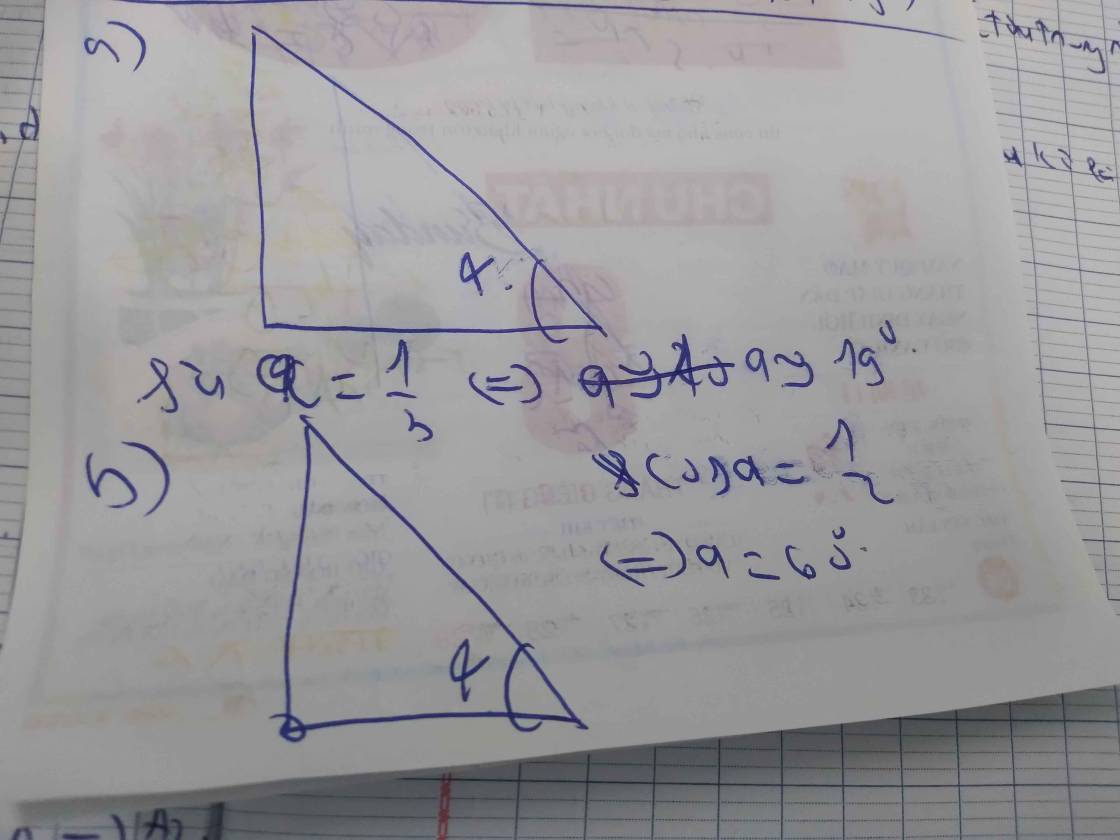
Dựng một tam giác vuông ta có:
a, Độ dài cạnh góc vuông là 3, cạnh huyền là 5, góc đối diện với cạnh góc vuông đó là góc α
b, Độ dài cạnh góc vuông là 4, cạnh huyền là 7,góc giữa cạnh góc vuông và cạnh huyền đó là góc α
c, Độ dài hai cạnh góc vuông là 3 và 2, góc đối diện với cạnh góc vuông độ dài 3 là góc α
d, Độ dài hai cạnh góc vuông là 5 và 6, góc đối diện với cạnh góc vuông độ dài 6 là góc α

ta có :\(\sin2=\dfrac{\sqrt{3}}{2}\Rightarrow2=60^0\)
\(\cos60^o=\dfrac{1}{2};\tan60^o=\sqrt{3};\cot60^o=\dfrac{1}{\sqrt{3}}\)

Có sin2a + cos2a = 1
Mà cos a = \(\dfrac{3}{4}\)
=> sin2a + (\(\dfrac{3}{4}\))2 = 1
=> sin2a + \(\dfrac{3^2}{4^2}\) = 1
=> sin2a + \(\dfrac{9}{16}\)= 1
=> sin2a = \(\dfrac{7}{16}\)
=> sin a = \(\dfrac{\sqrt{7}}{4}\)
Có tan a = \(\dfrac{\text{sin a}}{\text{cos a}}\)
Mà \(\left\{{}\begin{matrix}\text{cos a = }\dfrac{3}{4}\\\text{sin a = }\dfrac{\sqrt{7}}{4}\end{matrix}\right.\)
=> tan a = \(\dfrac{\dfrac{\sqrt{7}}{4}}{\dfrac{3}{4}}\) = \(\dfrac{\sqrt{7}}{4}\): \(\dfrac{3}{4}\) = \(\dfrac{\sqrt{7}}{4}\).\(\dfrac{4}{3}\) =\(\dfrac{\sqrt{7}}{3}\)
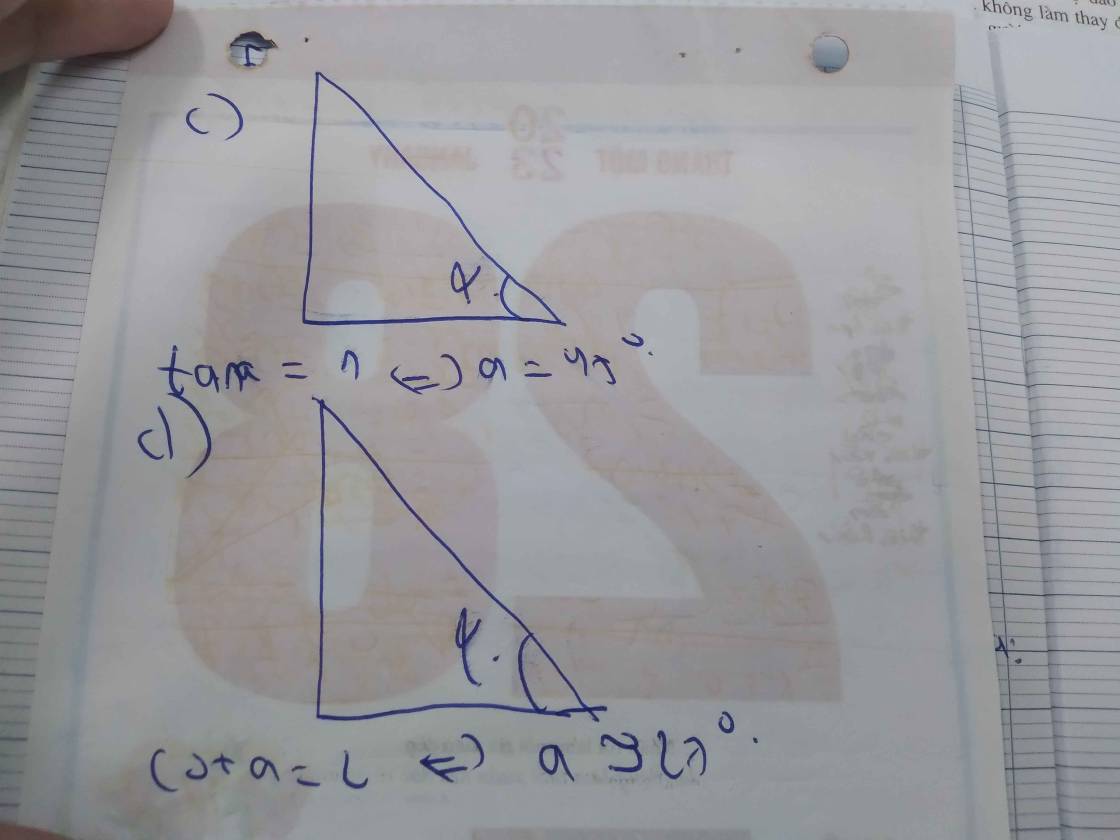

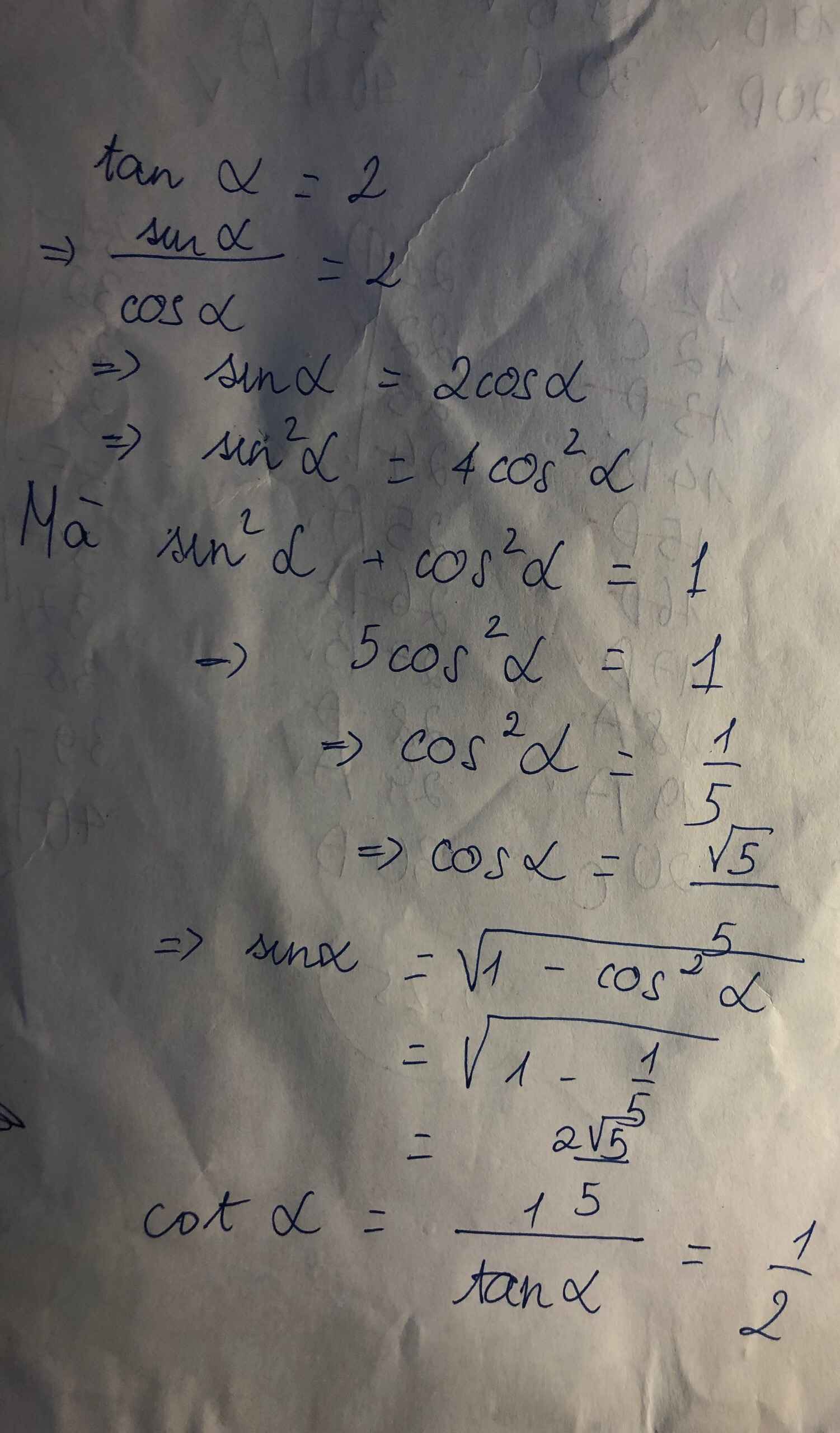
a: \(\cos\alpha=\dfrac{1}{2}\)
\(\tan\alpha=\sqrt{3}\)
\(\cot\alpha=\dfrac{\sqrt{3}}{3}\)