Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ĐKXĐ: \(x\ne1\)
Ta có: \(B=\dfrac{x^4-2x^3-3x^2+8x-1}{x^2-2x+1}\)
\(=\dfrac{x^4-2x^3+x^2-4x^2+8x-4+3}{x^2-2x+1}\)
\(=\dfrac{x^2\left(x^2-2x+1\right)-4\left(x^2-2x+1\right)+3}{x^2-2x+1}\)
\(=\dfrac{\left(x-1\right)^2\cdot\left(x^2-4\right)+3}{\left(x-1\right)^2}\)
\(=x^2-4+\dfrac{3}{\left(x-1\right)^2}\)
Để B nguyên thì \(3⋮\left(x-1\right)^2\)
\(\Leftrightarrow\left(x-1\right)^2\inƯ\left(3\right)\)
\(\Leftrightarrow\left(x-1\right)^2\in\left\{1;3;-1;-3\right\}\)
mà \(\left(x-1\right)^2>0\forall x\) thỏa mãn ĐKXĐ
nên \(\left(x-1\right)^2\in\left\{1;3\right\}\)
\(\Leftrightarrow x-1\in\left\{1;9\right\}\)
hay \(x\in\left\{2;10\right\}\) (nhận)
Vậy: \(x\in\left\{2;10\right\}\)

MK ko biế đúng ko nữa , sai thì ý kiến
a)
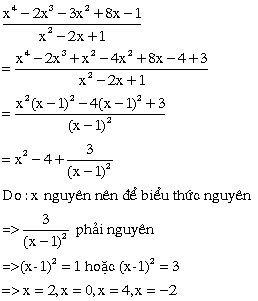
b)
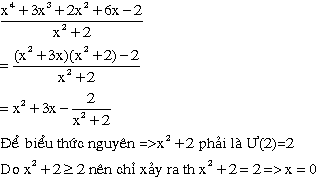
Chúc các bn hok tốt
Tham khảo nhé

a) ĐKXĐ: \(x\notin\left\{1;-1\right\}\)
b) Ta có: \(\dfrac{4x-4}{2x^2-2}\)
\(=\dfrac{4\left(x-1\right)}{2\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{2}{x+1}\)
Để phân thức có giá trị bằng -2 thì \(\dfrac{2}{x+1}=-2\)
\(\Leftrightarrow x+1=-1\)
hay x=-2(thỏa ĐK)

\(A=\frac{\left(x^4+4x^2+4\right)+\left(3x^3+6x\right)-\left(2x^2+4\right)-2}{x^2+2}\)
\(A=\frac{\left(x^2+2\right)^2+3x\left(x^2+2\right)-2\left(x^2+2\right)-2}{x^2+2}\)
\(A=\frac{\left(x^2+2\right)\left(x^2+3x\right)}{x^2+2}-\frac{2}{x^2+2}=x^2+3x-\frac{2}{x^2+2}\)
Để A là số nguyên, mà x là số nguyên nên \(x^2+3x\)nguyên, do đó \(\frac{2}{x^2+2}\inℤ\)
Do \(x^2+2\ge2\) nên \(x^2+2=2\Leftrightarrow x=0\)

phân thức được xác định ⇔ x2 - 1 ≠ 0 ⇔ x ≠ \(\left\{-1;1\right\}\)
\(\dfrac{3x+3}{x^2-1}=-2\)
=> 3x + 3 = -2x2 + 2
=> 2x2 + 3x + 1 = 0
=> (2x+1)(x+1) = 0
=> x = -1/2 (thỏa mãn) hoặc x = -1 (loại)
Vậy, để phân thức có giá trị bằng –2 thì x = -1/2.
\(\dfrac{3x+3}{x^2-1}\)=\(\dfrac{3\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}\) (x khác -1 và x khác 1)
= \(\dfrac{3}{x-1}\)
=> Phân thức ban đầu có giá trị nguyên ⇔ 3 chia hết cho x-1
=> x-1 ∈\(\left\{-3;-1;1;3\right\}\)
=> x ∈\(\left\{-2;0;2;4\right\}\)
Vậy, để phân thức có giá trị là số nguyên.thì x ∈\(\left\{-2;0;2;4\right\}\).
\(C=\dfrac{\left(x^2+3x\right)\left(x^2+2\right)-2}{x^2+2}=x^2+3x-\dfrac{2}{x^2+2}\)
\(C\in Z\Leftrightarrow2⋮\left(x^2+2\right)\)
\(\Leftrightarrow x^2+2=2\Rightarrow x=0\)