
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tìm 3 số tự nhiên a, b, c sao cho cả 3 số abc, ab + bc + ca và a + b + c + 2 đều là các số nguyên tố


Vì a, b, c có vai trũ như nhau nên giả sử a ≤ b ≤ c khi đó
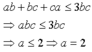
( Vì a là số nguyên tố )
Với a = 2 ta có
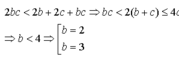
- Nếu b = 2 thì 4c < 2 + 4c thoả món với c là nguyên tố bất kỡ
- Nếu b = 3 thì 6c < 6b + 5c suy ra c < 6 vậy c = 3 hoặc c = 5
Vậy các cạp số (a, b, c) càn Tìm là (2, 2, p) ; (2, 3, 3 ) ; (2, 3, 5 ) và các hoán vị vủa chúng , với p là số nguyên tố .

\(\Leftrightarrow\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}>1\)
Do vai trò của a;b;c là như nhau, không mất tính tổng quát giả sử \(a< b< c\)
\(\Rightarrow\dfrac{1}{a}>\dfrac{1}{b}>\dfrac{1}{c}\Rightarrow\dfrac{3}{a}>\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}>1\)
\(\Rightarrow a< 3\Rightarrow a=2\)
Khi đó: \(\dfrac{1}{2}+\dfrac{1}{b}+\dfrac{1}{c}>1\Rightarrow\dfrac{1}{b}+\dfrac{1}{c}>\dfrac{1}{2}\)
\(\dfrac{2}{b}>\dfrac{1}{b}+\dfrac{1}{c}>\dfrac{1}{2}\Rightarrow b< 4\Rightarrow b=3\) (do \(b>a\Rightarrow b>2\))
Tiếp tục thay vào: \(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{c}>1\Rightarrow\dfrac{1}{c}>\dfrac{1}{6}\Rightarrow c< 6\)
Mà \(c>b\Rightarrow c>3\Rightarrow3< c< 6\Rightarrow c=5\)
Vậy \(\left(a;b;c\right)=\left(2;3;5\right)\) và các hoán vị

Đề bài cần nói rõ 3 số nguyên tố a,b,c khác nhau từng đôi một.
------------------------
abc < ab + bc + ac
<=> 1 < 1/a + 1/b + 1/c (*)
Chỉ có 6 bộ 3 số nguyên tố khác nhau thỏa mãn (*).Đó là (2;3;5); (2;5;3); (3;2;5); (3;5;2); (5;2;3); (5;3;2)
Trả lời : 6 (hoặc 1, nếu xem 6 bộ trên là như nhau)

abc < ab+bc+ac
<=> 1/a+1/b+1/c > 1 (*)
giả sử a > b >c => 1/a < 1/b <1/c
1 < 1/a +1/b +1/c < 1/c + 1/c + 1/c = 3/c => c < 3 => c = 2
thay c = 2 vào (*) được:
1/2 < 1/a + 1/b < 1/b + 1/b = 2/b => 2 < b < 4 => b = 3
thay b = 3; c = 2 vào (*) được:
1/a > 1 - 1/2 - 1/3 = 1/6 => 3 < a < 6 => a = 5
vậy bộ số (a;b;c) = (2;3;5) và các hoán vị của nó
Giả sử a≤b≤c⇒ab+bc+ca≤3bc. Theo giả thiết abc<ab+bc+ca (1) nên abc<3bc⇒a<3mà a là số nguyên tố nên a = 2. Thay a = 2 vào (1) được 2bc<2b+2c+bc⇒bc<2(b+c) (2)
Vì b≤c⇒bc<4c⇒b<4. Vì b là số nguyên tố nên b = 2 hoặc b = 3. Với b = 2 thay vào (2) được 2c < 4 + 2c đúng với mọi c là số nguyên tùy ý. Với b = 3 thay vào (2) được c < 6 nên c = 3 hoặc c = 5
Vậy (2; 2; c), (2; 3; 3), (2; 3; 5) với c là số nguyên tố tùy ý
\(\frac{2}{3}\)