Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1
Ta có: \(a.b=2018^{2018}\)
\(2018\equiv2\left(md3\right)\)
\(2018^{2018}\equiv2^{2018}\left(md3\right)\)
\(2018\equiv\left(2^2\right)^{1009}=4^{1009}\)
Mà \(4\equiv1\left(md3\right)\Rightarrow4^{1009}\equiv1\left(md3\right)\)
\(\Rightarrow a.b=2018^{2018}\equiv1\left(md3\right)\Rightarrow\orbr{\begin{cases}\hept{\begin{cases}a\equiv1\left(md3\right)\\b\equiv1\left(md3\right)\end{cases}}\\\hept{\begin{cases}a\equiv2\left(md3\right)\\b\equiv2\left(md3\right)\end{cases}}\end{cases}}\)
Khi đó:\(\orbr{\begin{cases}a+b\equiv2\left(md3\right)\\a+b\equiv1\left(md3\right)\end{cases}}\)
\(\Rightarrow a+b\)ko chia hết cho 3\(\Rightarrow a+b\)ko chia hết cho 2019
Vậy \(a+b\)ko chia hết cho 2019
Xin lỗi bạn nha ,máy mình bị liệt 1 s chữ , md là mod nha ! Hk t !

Vì a, b, c có vai trũ như nhau nên giả sử a ≤ b ≤ c khi đó
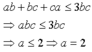
( Vì a là số nguyên tố )
Với a = 2 ta có
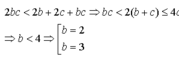
- Nếu b = 2 thì 4c < 2 + 4c thoả món với c là nguyên tố bất kỡ
- Nếu b = 3 thì 6c < 6b + 5c suy ra c < 6 vậy c = 3 hoặc c = 5
Vậy các cạp số (a, b, c) càn Tìm là (2, 2, p) ; (2, 3, 3 ) ; (2, 3, 5 ) và các hoán vị vủa chúng , với p là số nguyên tố .

Giả sử a≤b≤c⇒ab+bc+ca≤3bc. Theo giả thiết abc<ab+bc+ca (1) nên abc<3bc⇒a<3mà a là số nguyên tố nên a = 2. Thay a = 2 vào (1) được 2bc<2b+2c+bc⇒bc<2(b+c) (2)
Vì b≤c⇒bc<4c⇒b<4. Vì b là số nguyên tố nên b = 2 hoặc b = 3. Với b = 2 thay vào (2) được 2c < 4 + 2c đúng với mọi c là số nguyên tùy ý. Với b = 3 thay vào (2) được c < 6 nên c = 3 hoặc c = 5
Vậy (2; 2; c), (2; 3; 3), (2; 3; 5) với c là số nguyên tố tùy ý