
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án B
Điều kiện: 2 x − x 2 > 0 2 − x 2 > 0 ⇔ 0 < x < 2 ⇒ D = 0 ; 2
Phương trình
⇔ a 2 + 4 a + 5 log 3 2 x − x 2 + 9 a 2 − 6 a + 2 log 11 1 − x 2 2
= log 3 2 x − x 2 + log 11 1 − x 2 2
⇔ f x = a + 2 2 log 3 2 x − x 2 + 3 a − 1 2 log 11 1 − x 2 2 = 0
⇔ f x = a 2 + 4 a + 4 log 3 2 x − x 2 + 9 a 2 − 6 a + 2 log 11 1 − x 2 2
= log 3 2 x − x 2 + log 11 1 − x 2 2 = 0 x ∈ 0 ; 2
⇔ f x = a + 2 2 log 3 2 x − x 2 + 3 a − 1 2 log 11 1 − x 2 2 = 0
Ta có:
f ' x = a + 2 2 . 2 − 2 x 2 x − x 2 ln 3 + 3 a − 1 2 . 1 − x 1 = x 2 2 ln 11 = 0
⇔ x = 1
Ta có:
lim x → 0 f x = − ∞ ; f 1 = − 3 a − 1 2 log 11 2 ; lim x → 2 f x = − ∞ ⇒ phương trình đã cho có nghiệm duy nhất khi − 3 a − 1 2 log 11 2 = 0 ⇔ a = 1 3 ∉ ℤ

Đáp án A
Gọi I là điểm sao cho 4 I A → + 3 I B → + 5 I C → = 0 → ⇒ I − 1 6 ; 1 12 ; 1 3
M A → . M B → + 2 M B → . M C → + 3 M C → . M A → = I A → − I M → I B → − I M → + 2 I B → − I M → I C → − I M → + 3 I C → − I M → I A → − I M → = I A → . I B → + 2 I B → . I C → + 3 I C → . I A → − I M → 4 I A → + 3 I B → + 5 I C → + 6 I M 2
Do I A → . I B → + 2 I B → . I C → + 3 I C → . I A → là hằng số và I M → 4 I A → + 3 I B → + 5 I C → = 0 Nên S min k h i I M min ⇔ M là hình chiếu của I lên mặt phẳng O x y ⇒ M − 1 6 ; 1 12 ; 0 ⇒ T = − 2 + 1 = − 1

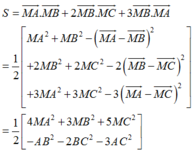
Xác định tọa độ điểm I(m,n,p) sao cho
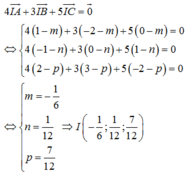
Khi đó:

đạt giá trị nhỏ nhất khi và chỉ khi MI ngắn nhất M là hình chiếu của I lên (Oxy)
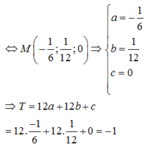
Chọn: D

Từ a - b = 7 hay a = b+7 do đó nếu a chia hết cho 7 thì b cũng chia hết cho 7 và ngược lại. (*)
Lại có BCNN(a,b) = 140 suy ra: a hoặc b chia hết cho 7 (vì 7 là ước của 140). (**)
Từ (*)(**) suy ra a và b đều chia hết cho 7.
Đặt b=7k (k nguyên dương) suy ra a = 7(k+1)
khi đó BCNN(a;b) = BCNN(7(k+1),7k) = 140
hay BCNN(k+1;k) = 20 (chia 2 vế cho 7)
tương đương k(k+1) = 20 (vì UCLN(k+1;k) = 1)
Giải ra k = 4, suy ra b = 28; a = 35
Vậy 2 số phải tìm là: a = 35 và b = 28
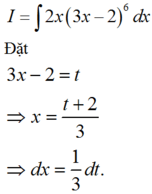
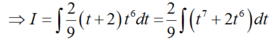
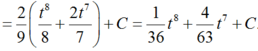
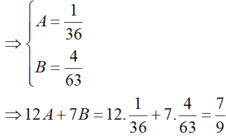



-4 và -3
-4;-3