NT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
19 tháng 9 2023
Số tập con có 3 phần tử trong đó luôn có số 1 là bạn tìm số cách lấy 2 số từ 5 số còn lại, trừ số 1 ra
=>Có \(C^2_5=10\left(cách\right)\)
N
18 tháng 9 2019
1/ B={x ∈ R| (9-x2)(x2-3x+2)=0}
Ta có:
(9-x2)(x2-3x+2)=0
⇔\(\left[{}\begin{matrix}9-x^2=0\\x^2-3x+2=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left(3+x\right)\left(3-x\right)=0\\\left(x^2-x\right)-\left(2x-2\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\pm3\\x\left(x-1\right)-2\left(x-1\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\pm3\\\left(x-1\right)\left(x-2\right)=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\pm3\\x=1\\x=2\end{matrix}\right.\)
⇒B={-3;1;2;3}
2/ Có 15 tập hợp con có 2 phần tử
NM
[1] Cho tập hợp A = { -1; 0; 1; 2; 3 }. Số tập con gồm 2 phân tử của tập A là
A. 20 B. 10 C. 12 D. 15
1
H9
HT.Phong (9A5)
CTVHS
17 tháng 8 2023
Các tập hợp có thể lập được là:
\(B=\left\{-1;0\right\}\); \(C=\left\{-1;1\right\}\); \(D=\left\{-1;2\right\}\); \(E=\left\{-1;3\right\}\); \(F=\left\{0;1\right\}\); \(G=\left\{0;2\right\}\); \(H=\left\{0;3\right\}\); \(I=\left\{1;2\right\}\); \(J=\left\{1;3\right\}\); \(L=\left\{2;3\right\}\)
Số tập hợp lập được là 10 tập hợp
⇒ Chọn B
5 tháng 4 2017
1. a) Tập hợp con của A: {a} và \(\varnothing\)
b) Tập hợp con của B: {a}; {b}; {a;b} và \(\varnothing\)
c) Tập hợp con: \(\varnothing\)
2. a) A có 1 phần tử thì A sẽ có: 21=2 (tập hợp con)
b) A có 2 phần tử thì A sẽ có: 22=4 (tập hợp con)
c) A có 3 phần tử thì A sẽ có: 23=8 (tập hợp con)
*Cách tính số tập hợp con: Nếu tập hợp A có n phần tử thì A sẽ có 2n tập hợp con.
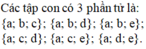
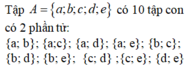
Câu B
Đó là:{1;2},{1;3},{1;4},{1;5},{1;6},{2;3},{2;4},{2;5},{2;6},{3;4},{3;5},{3;6},{4;5},{4;6},{5;6}
Đúng cho mình 1 k nha <3