

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



tự vẽ hình
ta có <HBA+<BAH= 90\(^0\)(vì tam giác ABH vg tại H)
Có <BAH+ <HAC= 90\(^0\)(vì tam giác ABC vg tại A)
=> <HBA=<HAC
Xét tam giác BAH và ACH
<BHA=<AHC\(\left(90^0\right)\)
<ABH=<HAC
=> Tam giác BAH đồng dạng với tam giác ACH
=> BH/AH=AH/CH=> AH^2= BH*CH=4*9=36 cm
b, ta có BC=BH+CH=4+9=13 cm
S(ABC) = AH*BC=36*13=468 cm\(^2\)

a) Xét tam giác ABC : AB2+AC2= 32+42=9+16=25(cm) và BC2= 52= 25 => AB2+AC2=BC2(=25) =>tam giác ABC vuông tại A (định lí pi-ta-go đảo)
+) Xét tam giác AHB và tam giác CHA:
góc AHB = góc CHA(=900)
góc BAH = góc ACH ( cùng phụ với góc HAC)
=> tam giác AHB ~ tam giác CHA ( g-g)
+) Xét tam giác HCA và tam giác ACB:
góc AHC = góc BAC(=900)
góc ACB chung
=> tam giác HCA ~ tam giác ACB (g-g)
b) Có: tam giác HCA ~ tam giác ACB(phần a) => AH/AB = AC/BC => AH/3 = 4/5 => AH= 4/5x3 = 2,4 (cm)
Áp dụng định lí Pi-ta-go trong tam giác AHB vuông tại H :
AH2+BH2 = AB2 <=> 2,42+ BH2 = 32 <=> 5,76+BH2 = 9 <=> BH2 = 9-5,76 <=> BH2 = 3,24 <=>. BH= căn 3,24 <=> BH =1,8 (cm)
Có: tam giác AHB ~ tam giác CHA( phần a) => AH/HC = BH/AH <=> AH2 = BHxHC <=> 2,42 = 1,8+HC <=> HC= 5,76-1,8 <=> HC=3,96 (cm)
Vậy AH=2,4cm; BH=1,8cm; HC=3,96cm
CÒN CÂU C THÌ MIK KO BIẾT. :P

a: BC=5cm
b: Xét ΔHBA vuông tại H và ΔHAC vuông tại H có
\(\widehat{HBA}=\widehat{HAC}\)
Do đó: ΔHBA\(\sim\)ΔHAC
c: Ta có: ΔHBA\(\sim\)ΔHAC
nên HB/HA=HA/HC
hay \(HA^2=HB\cdot HC\)
d: Xét ΔABC có AD là phân giác
nên BD/AB=CD/AC
hay BD/3=CD/4
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BD}{3}=\dfrac{CD}{4}=\dfrac{BD+CD}{3+4}=\dfrac{5}{7}\)
Do đó: BD=15/7(cm); CD=20/7(cm)

a: BC=5cm
b: Xét ΔHBA vuông tại H và ΔHAC vuông tại H có
góc HBA=góc HAC
=>ΔHBA đồng dạng với ΔHAC
c: ΔHBA đồng dạng với ΔHAC
=>HB/HA=HA/HC
=>HA^2=HB*HC

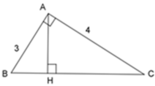
Áp dụng định lý Pytago vào tam giác vuông ABC ta có:
A B 2 + A C 2 = B C 2 ⇔ 3 2 + 4 2 = B C 2
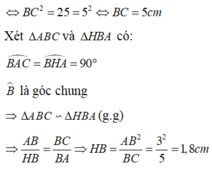


a, Xét tam giác ABH và tam giác CAH ta có :
^AHB = ^CHA = 900
^BAH = ^HCA ( cùng phụ ^HAC )
Vậy tam giác ABH ~ tam giác CAH ( g.g )
b, Xét tam giác ABC vuông tại A, đường cao AH
Áp dụng định lí Pytago cho tam giác AHB vuông tại H
\(AB^2=BH^2+AH^2\Rightarrow BH^2=AB^2-AH^2=225-144=81\Rightarrow BH=9\)cm
* Áp dụng hệ thức :
\(AH^2=BH.HC\Rightarrow HC=\dfrac{AH^2}{BH}=\dfrac{144}{9}=16\)cm
=> BC = HC + HB = 16 + 9 = 25 cm
* Áp dụng hệ thức : \(AH.BC=AB.AC\Rightarrow AC=\dfrac{AH.BC}{AB}=\dfrac{12.25}{15}=20\)cm
a) Xét ΔBHA vuông tại H và ΔAHC vuông tại H có
\(\widehat{BAH}=\widehat{ACH}\left(=90^0-\widehat{B}\right)\)
Do đó: ΔBHA\(\sim\)ΔAHC(g-g)