VE
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
7 tháng 8 2021
Ta có \(\left(\sqrt{2018}+\sqrt{2020}\right)^2=4038+2\sqrt{4076360}\) và \(\left(2\sqrt{2019}\right)^2=8076=4038+4038\)
Mà \(\left(2\sqrt{4076360}\right)^2=16305440\) và \(4038^2=16305444\)
\(\Rightarrow2\sqrt{4076360}< 4038\)
\(\Rightarrow\sqrt{2018}+\sqrt{2020}< 2\sqrt{2019}\)
7 tháng 8 2021
\(\left(\sqrt{2018}+\sqrt{2020}\right)^2=4038+2\cdot\sqrt{2018\cdot2020}\)
\(\left(2\sqrt{2019}\right)^2=8076=4038+4038\)
mà \(2\cdot\sqrt{2018\cdot2020}< 4038\)
nên \(\sqrt{2018}+\sqrt{2020}< 2\sqrt{2019}\)
VT
1
10 tháng 10 2018
Đặt \(A=\left(\sqrt{2018}+\sqrt{2020}\right)\)
\(\Rightarrow A^2=2018+2\sqrt{2018.2020}+2020=4038+\sqrt{4.2018.2020}=4038+\sqrt{4.\left(2019^2-1\right)}\)
Đặt \(B=2\sqrt{2019}=\sqrt{4.2019}\)
\(B^2=4.2019=2.2019+2.2019=4038+\sqrt{4.2019^2}\)
=> \(\sqrt{4.2019^2}>\sqrt{4.\left(2019^2-1\right)}\)
\(\Rightarrow A>B\Leftrightarrow\sqrt{2018}+\sqrt{2020}>2\sqrt{2019}\)
AH
Akai Haruma
Giáo viên
7 tháng 8 2021
Lời giải:
$\sqrt{15}< \sqrt{16}=4$
$\sqrt{17}< \sqrt{25}=5$
$\Rightarrow \sqrt{15}+\sqrt{17}< 9< 16$
NT
4
KN
2 tháng 8 2019
Giả sử \(8< \sqrt{15}+\sqrt{17}\)
\(\Leftrightarrow64< 15+2\sqrt{15.17}+17\)(Bình phương hai vế)
\(\Leftrightarrow32< 2\sqrt{15.17}\)
\(\Leftrightarrow16< \sqrt{15.17}\)
\(\Leftrightarrow16< \sqrt{\left(16-1\right)\left(16+1\right)}\)
\(\Leftrightarrow\sqrt{16^2}< \sqrt{16^2-1}\)
\(\Leftrightarrow16^2< 16^2-1\)(vô lí)
Chứng minh tương tự điều giả sử \(8=\sqrt{15}+\sqrt{17}\)
Vậy \(8>\sqrt{15}+\sqrt{17}\)
2 tháng 8 2019
https://olm.vn/hoi-dap/detail/61596070678.html
bn coppy link này nhé, có bài mak bn đang cần đấy
PT
1
LT
2
24 tháng 10 2016
Giả sử \(8>\sqrt{15}+\sqrt{17}\)
\(\Leftrightarrow64>32+2\sqrt{15×17}\)
\(\Leftrightarrow16>\sqrt{\left(16-1\right)\left(16+1\right)}=\sqrt{16^2-1}\left(dung\right)\)
Vậy \(8>\sqrt{15}+\sqrt{17}\)
8 tháng 10 2018
dsadasdsadsadsasddấdasdasdadấdadsdsđasdasđdsaádasdasdádaddadadaddadadaddâdadaad
19 tháng 9 2021
\(a,\left(\sqrt{\sqrt{3}}\right)^4=3< 4=\left(\sqrt{2}\right)^4\Rightarrow\sqrt{\sqrt{3}}< \sqrt{2}\\ b,\left(\sqrt{2\sqrt{3}}\right)^4=12< 18=\left(\sqrt{3\sqrt{2}}\right)^4\Rightarrow\sqrt{2\sqrt{3}}=\sqrt{3\sqrt{2}}\\ c,\left(2+\sqrt{6}\right)^2=8+4\sqrt{6};5^2=25=8+17;\left(4\sqrt{6}\right)^2=96< 289=17^2\\ \Rightarrow4\sqrt{6}< 17\Rightarrow2+\sqrt{6}< 5\\ d,\left(7-2\sqrt{2}\right)^2=57-28\sqrt{2};4^2=16=57-41;\left(28\sqrt{2}\right)^2=1568< 41^2=1681\\ \Rightarrow28\sqrt{2}< 41\Rightarrow7-2\sqrt{2}>4\\ e,\left(\sqrt{15}+\sqrt{8}\right)^2=23+4\sqrt{30};7^2=49=23+26;\left(4\sqrt{30}\right)^2=240< 676=26^2\\ \Rightarrow4\sqrt{30}< 26\Rightarrow\sqrt{15}+\sqrt{8}< 7\)
\(f,\left(\sqrt{37}-\sqrt{14}\right)^2=51-2\sqrt{518};\left(6-\sqrt{15}\right)^2=51-12\sqrt{15};\left(2\sqrt{518}\right)^2=2072;\left(12\sqrt{15}\right)^2=2160\\ \Rightarrow2\sqrt{518}< 12\sqrt{15}\Rightarrow\sqrt{37}-\sqrt{14}>6-\sqrt{15}\)
19 tháng 10 2020
\(^6\sqrt{2019} = b, ^6\sqrt{2020} = a \\ Then, A = a^3 - b^3; B = a^2 -b^2\\ \Rightarrow A > B \)
19 tháng 9 2021
a) \(1=\sqrt{1}< \sqrt{2}\)
b) \(2=\sqrt{4}>\sqrt{3}\)
c) \(6=\sqrt{36}< \sqrt{41}\)
d) \(7=\sqrt{49}>\sqrt{47}\)
e) \(2=1+1=\sqrt{1}+1< \sqrt{2}+1\)
f) \(1=2-1=\sqrt{4}-1>\sqrt{3}-1\)
g) \(2\sqrt{31}=\sqrt{4.31}=\sqrt{124}>\sqrt{100}=10\)
h) \(\sqrt{3}>0>-\sqrt{12}\)
i) \(5=\sqrt{25}< \sqrt{29}\)
\(\Rightarrow-5>-\sqrt{29}\)
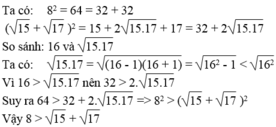
\(8^2=64=32+2\sqrt{16^2}\)
\(\left(\sqrt{15}+\sqrt{17}\right)^2=32+2\sqrt{15.17}=32+2\sqrt{\left(16-1\right)\left(16+1\right)}\)
\(=32+2\sqrt{16^2-1}\)
\(< =>8^2>\left(\sqrt{15}+\sqrt{17}\right)^2\)
\(8>\sqrt{15}+\sqrt{17}\)
\(\left(\sqrt{2019}+\sqrt{2021}\right)^2=4040+2\sqrt{2019.2021}\)
\(=4040+2\sqrt{\left(2020-1\right)\left(2020+1\right)}=4040+2\sqrt{2020^2-1}\)
\(\left(2\sqrt{2020}\right)^2=8080=4040+2\sqrt{2020^2}\)
\(< =>\sqrt{2019}+\sqrt{2021}< 2\sqrt{2020}\)
mik chọn điền
<
mik lười chép ại đề bài