
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(243^5=\left(3^5\right)^5=3^{25}=3\cdot3^{24}=3\cdot\left(3^3\right)^8=3\cdot27^8\)
\(243^5=3^{25}\)
\(3\cdot27^8=3\cdot3^{24}=3^{25}\)
Do đó: \(243^5=3\cdot27^8\)



1512 = 312.512
274.256 = (33)4.(52)6
274 = 312.512
1512 = 274.256


a: 13/67=91/469>91/470
b: 141/813=22419/129267
159/904=22419/127464
=>141/813<159/904

a) \(243^5=\left(3^5\right)^5=3^{25}\)
\(3\cdot27^5=3\cdot\left(3^3\right)^5=3\cdot3^{15}=3^{16}\)
mà \(3^{25}>3^{16}\)
nên \(243^5>3\cdot27^5\)
b) \(625^5=\left(5^4\right)^5=5^{20}\)
\(125^7=\left(5^3\right)^7=5^{21}\)
mà \(5^{20}< 5^{21}\)
nên \(625^5< 125^7\)
c) \(202^{303}=\left(202^3\right)^{101}=8242408^{101}\)
\(303^{202}=\left(303^2\right)^{101}=91809^{101}\)
mà \(8242408^{101}>91809^{101}\)
nên \(202^{303}>303^{202}\)

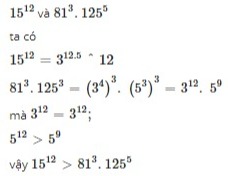
a.
2435 = (35)5 = 325
278 x 3 = (33)8 x 3 = 324 x 3 = 325
vì 325 = 325
=> 2435 = 3 x 278
b.
1512 = (3 x 5)12 = 312 x 512
813 = (34)3 = 312
1255 = (53)5 = 515
ta so sánh 312 x 512 với 312 x 515
312 = 312
512 < 515
=> 312 x 512 < 312 x 515
=> 1512 < 813 x 1255
Cảm ơn