Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
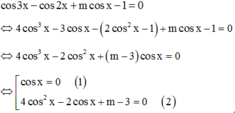
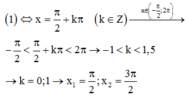
→
(1) có 2 nghiệm thuộc 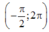
Để phương trình có đúng 8 nghiệm thuộc khoảng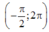 thì (2) phải có đúng 6 nghiệm phân biệt thuộc
thì (2) phải có đúng 6 nghiệm phân biệt thuộc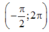 và khác
x
1
;
x
2
và khác
x
1
;
x
2
Đặt t = cos x ( - 1 ≤ x ≤ 1 ) , (2) trở thành f ( t ) = 4 t 2 - 2 t + m - 3 = 0 ( 3 )
+ Nếu
0
<
t
<
1
thì phương trình cosx=t có 3 nghiệm phân biệt thuộc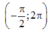
+ Nếu
-
1
<
t
<
0
thì phương trình cosx=t có 2 nghiệm phân biệt thuộc khoảng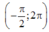
Do đó (2) có đúng 6 nghiệm phân biệt thuộc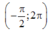
⇔ (3) có 2 nghiệm t 1 ; t 2 thỏa mãn 0 < t 1 < t 2 < 1
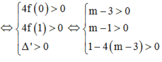


1.
\(cos2x-3cosx+2=0\)
\(\Leftrightarrow2cos^2x-3cosx+1=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=1\\cosx=\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k2\pi\\x=\pm\dfrac{\pi}{3}+k2\pi\end{matrix}\right.\)
\(x=k2\pi\in\left[\dfrac{\pi}{4};\dfrac{7\pi}{4}\right]\Rightarrow\) không có nghiệm x thuộc đoạn
\(x=\pm\dfrac{\pi}{3}+k2\pi\in\left[\dfrac{\pi}{4};\dfrac{7\pi}{4}\right]\Rightarrow x_1=\dfrac{\pi}{3};x_2=\dfrac{5\pi}{3}\)
\(\Rightarrow P=x_1.x_2=\dfrac{5\pi^2}{9}\)
2.
\(pt\Leftrightarrow\left(cos3x-m+2\right)\left(2cos3x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos3x=\dfrac{1}{2}\left(1\right)\\cos3x=m-2\left(2\right)\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow x=\pm\dfrac{\pi}{9}+\dfrac{k2\pi}{3}\)
Ta có: \(x=\pm\dfrac{\pi}{9}+\dfrac{k2\pi}{3}\in\left(-\dfrac{\pi}{6};\dfrac{\pi}{3}\right)\Rightarrow x=\pm\dfrac{\pi}{9}\)
Yêu cầu bài toán thỏa mãn khi \(\left(2\right)\) có nghiệm duy nhất thuộc \(\left(-\dfrac{\pi}{6};\dfrac{\pi}{3}\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}m-2=0\\m-2=1\\m-2=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=2\\m=3\\m=1\end{matrix}\right.\)
TH1: \(m=2\)
\(\left(2\right)\Leftrightarrow cos3x=0\Leftrightarrow x=\dfrac{\pi}{6}+\dfrac{k2\pi}{3}\in\left(-\dfrac{\pi}{6};\dfrac{\pi}{3}\right)\Rightarrow x=\dfrac{\pi}{6}\left(tm\right)\)
\(\Rightarrow m=2\) thỏa mãn yêu cầu bài toán
TH2: \(m=3\)
\(\left(2\right)\Leftrightarrow cos3x=0\Leftrightarrow x=\dfrac{k2\pi}{3}\in\left(-\dfrac{\pi}{6};\dfrac{\pi}{3}\right)\Rightarrow x=0\left(tm\right)\)
\(\Rightarrow m=3\) thỏa mãn yêu cầu bài toán
TH3: \(m=1\)
\(\left(2\right)\Leftrightarrow cos3x=-1\Leftrightarrow x=\dfrac{\pi}{3}+\dfrac{k2\pi}{3}\in\left(-\dfrac{\pi}{6};\dfrac{\pi}{3}\right)\Rightarrow\left[{}\begin{matrix}x=\pm\dfrac{1}{3}\\x=-1\\x=-\dfrac{5}{3}\end{matrix}\right.\)
\(\Rightarrow m=2\) không thỏa mãn yêu cầu bài toán
Vậy \(m=2;m=3\)

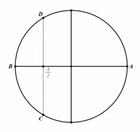

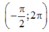 . Tính tổng T=a+b
. Tính tổng T=a+b
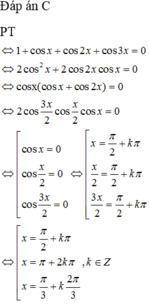
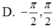

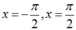
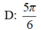

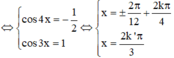
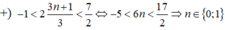

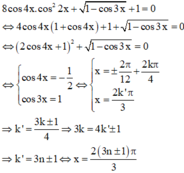

Chọn D
Phương trình tương với:
Trên đường tròn đơn vị, các điểm nghiệm của phương trình là 4 điểm A, B, C, D như hình vẽ. Do đó trên nửa khoảng [ - π ; 0 ) , phương trình có đúng 2 nghiệm (là - π và - 2 π 3 ).