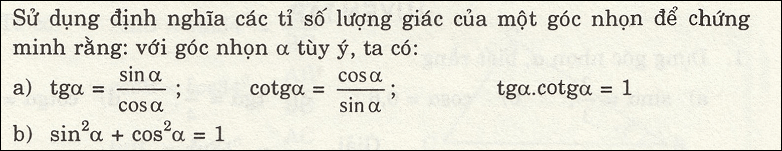Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(cos32=sin58;cos53=sin37;cos8=sin82\)
18<37<44<58<82
=>\(sin18< sin37< sin44< sin58< sin82\)
=>\(sin18< cos53< sin44< cos32< cos8\)
b: 20<45
=>\(sin20< tan20\)
\(cot8=tan82;cot37=tan53\)
20<40<53<82
=>\(tan20< tan40< tan53< tan82\)
=>\(tan20< tan40< cot37< cot8\)
=>\(sin20< tan20< tan40< cot37< cot8\)

Thứ tự tăng dần :
1) cos 62 độ 25 phút; sin 35 độ; cos 47 độ; sin 53 độ 30 phút; sin 74 độ.
2) tan 11 độ; cot 63 độ = tan 27 độ; cot 57 độ 30 phút; tan 55 độ

\(A=sin42^0-cos48^0=cos\left(90^0-42^0\right)-cos48^0=cos48^0-cos48^0=0\)
\(B=cot56^0-tan34^0=tan\left(90^0-56^0\right)-tan34^0=tan34^0-tan34^0=0\)
\(C=sin30^0-cot50^0-cos60^0+tan40^0\)
\(=cos\left(90^0-30^0\right)-tan\left(90^0-50^0\right)-cos60^0+tan40^0\)
\(=cos60^0-tan40^0-cos60^0+tan40^0=0\)
\(A=\sin42^0-\cos48^0=\sin42^0-\sin42^0=0\)
\(B=\cot56^0-\tan34^0=\tan34^0-\tan34^0=0\)

đáp án
A=Sin 42o - cos 48o =cos(90o - 42o) - cos 48o= cos48o - cos48o=0
hok tốt
B=cos56o-tan34o=tan(90o - 56o) - tan34o=tan34o - tan34o=0

a, theo tỉ số lượng giác, ta có: \(\sin\alpha=\cos90-\alpha\)
=> cos28 = sin62 , cos88 = sin2 , cos20 = sin 70
mà sin của góc càng lớn giá trị càng lớn .=> sin2 , sin40 , sin62 , sin 65 , sin70
hay cos88 , sin 40 , cos28 , sin65 , cos 20
câu b làm tương tự nha bạn (1độ = 100')
à mà quên là \(\tan\alpha=\cot90-\alpha\)
và giá trị của tan cũng tăng theo giá trị góc như sin

a) sin 40, cos 28, sin 65, cos88, cos20
ta có: \(cos28^0=sin62^0\)
\(cos88^0=sin2^0\)
\(cos20^0=sin70^0\)
vì \(sin2^0< sin40^0< sin62^0< sin65^0< sin70^0\)
nên \(cos88^0< sin40^0< cos28^0< sin65^0< cos20^0\)
b) \(tan32^048',cot28^036',tan56^032',cot67^018'\)
ta co: \(cot28^036'=tan62^036'\approx tan63^0\)
\(cot67^018'=tan23^018'\approx tan23^0\)
\(tan32^048'\approx tan33^0\)
\(tan56^032'\approx tan57^0\)
vi \(tan23^0< tan33^0< tan57^0< tan63^0\)
nen \(cot67^018'< tan32^048'< tan56^032'< cot28^036'\)

Bài 1:
\(\cos60^0=\sin30^0;\sin67^0=\cos23^0;\tan80^0=\cot10^0;\cot20^0=\cot20^0\)
Bài 2:
Xét tam giác ABC vuông tại A
\(a,\dfrac{\sin\alpha}{\cos\alpha}=\dfrac{AC}{BC}:\dfrac{AB}{BC}=\dfrac{AC}{AB}=\tan\alpha\\ \cot\alpha=\dfrac{1}{\tan\alpha}=\dfrac{1}{\dfrac{\sin\alpha}{\cos\alpha}}=\dfrac{\cos\alpha}{\sin\alpha}\\ \tan\alpha\cdot\cot\alpha=\dfrac{AC}{AB}\cdot\dfrac{AB}{AC}=1\\ b,\sin^2\alpha+\cos^2\alpha=\dfrac{AC^2}{BC^2}+\dfrac{AB^2}{BC^2}=\dfrac{AB^2+AC^2}{BC^2}=\dfrac{BC^2}{BC^2}=1\left(định.lí.pytago\right)\)