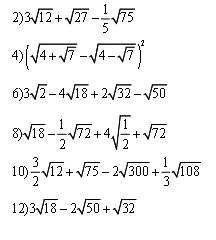Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\left(2\sqrt{3}+\sqrt{5}\right).\sqrt{3}-\sqrt{60}\)
\(=\)\(2\sqrt{3}.\sqrt{3}+\sqrt{5}.\sqrt{3}-\sqrt{60}\)
\(=\)\(6+\sqrt{15}-\sqrt{60}\)
\(=\)\(6-\sqrt{15}\)
\(\left(2\sqrt{3}+\sqrt{5}\right)\sqrt{3}-\sqrt{60}\)
=\(6+\sqrt{15}-\sqrt{2^2.15}\)
=\(6+\sqrt{15}-2\sqrt{15}\)
=\(6-\sqrt{15}\)
k mk nha

Lời giải:
ĐKXĐ: $x>0; x\neq 1$
\(P=\frac{1}{\sqrt{x}+1}+\frac{x}{\sqrt{x}(1-\sqrt{x})}=\frac{1}{\sqrt{x}+1}+\frac{\sqrt{x}}{1-\sqrt{x}}\)
\(=\frac{1-\sqrt{x}+\sqrt{x}(\sqrt{x}+1)}{(\sqrt{x}+1)(1-\sqrt{x})}=\frac{x+1}{1-x}\)
b. Khi $x=\frac{1}{\sqrt{2}}$ thì:
\(P=\frac{\frac{1}{\sqrt{2}}+1}{1-\frac{1}{\sqrt{2}}}=3+2\sqrt{2}\)

\(A=2\sqrt{27}-\sqrt{75}-\sqrt{\frac{4}{3}}\)\(=2\sqrt{9.3}-\sqrt{25.3}-\sqrt{\frac{4.3}{9}}\)\(=2.3\sqrt{3}-5\sqrt{3}-\frac{2}{3}\sqrt{3}\)\(=6\sqrt{3}-5\sqrt{3}-\frac{2}{3}\sqrt{3}\)\(=\frac{1}{3}\sqrt{3}\)\(=\frac{\sqrt{3}}{3}\)

2: \(=6\sqrt{3}+3\sqrt{3}-\sqrt{3}=8\sqrt{3}\)
4:
\(=4+\sqrt{7}+4-\sqrt{7}-2\sqrt{16-7}=8-2\cdot3=2\)
6: \(=3\sqrt{2}-12\sqrt{2}+8\sqrt{2}-5\sqrt{2}=-6\sqrt{2}\)
8: \(=3\sqrt{2}-3\sqrt{2}+2\sqrt{2}+6\sqrt{2}=8\sqrt{2}\)
10: \(=3\sqrt{3}+5\sqrt{3}-20\sqrt{3}+2\sqrt{3}=-10\sqrt{3}\)
12: \(=9\sqrt{2}-10\sqrt{2}+4\sqrt{2}=3\sqrt{2}\)

C=\(\left(\frac{\sqrt{x}+2}{\left(\sqrt{x}+1\right)^2}-\frac{\sqrt{x}-1}{\left(\sqrt{x}+1\right).\left(\sqrt{x}-1\right)}\right).\frac{\sqrt{x}+1}{\sqrt{x}}\)
C=\(\frac{\left(\sqrt{x}+2\right).\left(x-1\right)-\left(\sqrt{x}-1\right).\left(\sqrt{x}+1\right)}{\left(\sqrt{x}+1\right)^2.\left(x-1\right)}.\frac{\sqrt{x}+1}{\sqrt{x}}\)
C=\(\frac{x\sqrt{x}-\sqrt{x}+2x-2-\left(x-1\right)}{\left(\sqrt{x}+1\right)^2.\left(x-1\right)}.\frac{\sqrt{x}+1}{\sqrt{x}}\)
C=\(\frac{x-1+x\sqrt{x}-\sqrt{x}}{\left(\sqrt{x}+1\right)^2.\left(x-1\right)}.\frac{\sqrt{x}+1}{\sqrt{x}}\)
C=\(\frac{\left(x-1\right).\left(\sqrt{x}+1\right)}{\left(\sqrt{x}+1\right)^2.\left(x-1\right)}.\frac{\sqrt{x}+1}{\sqrt{x}}\)
C=\(\frac{1}{\sqrt{x}}=\frac{\sqrt{x}}{x}\)

a) \(A=\sqrt{9a}-\sqrt{16a}-\sqrt{49a}=3\sqrt{a}-4\sqrt{a}-7\sqrt{a}=-8\sqrt{a}\)
b) \(B=\dfrac{3+2\sqrt{3}}{\sqrt{3}}+\dfrac{2+\sqrt{2}}{\sqrt{2}}-\left(\sqrt{3}+\sqrt{2}\right)\)
\(=\dfrac{\sqrt{3}\left(2+\sqrt{3}\right)}{\sqrt{3}}+\dfrac{\sqrt{2}\left(\sqrt{2}+1\right)}{\sqrt{2}}-\left(\sqrt{3}+\sqrt{2}\right)\)
\(=2+\sqrt{3}+\sqrt{2}+1-\sqrt{3}-\sqrt{2}=3\)

ĐK: x > 0
a) Rút gọn M
M = \(\frac{\sqrt{x}}{x+\sqrt{x}}:\left(\frac{1}{\sqrt{x}}+\frac{\sqrt{x}}{\sqrt{x}+1}\right)\)
= \(\frac{\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+1\right)}:\left(\frac{\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}+1\right)}+\frac{\sqrt{x}.\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+1\right)}\right)\)
= \(\frac{\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+1\right)}:\left(\frac{x+\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}+1\right)}\right)\)
\(=\frac{\sqrt{x}}{x+\sqrt{x}+1}\)
b) \(\frac{1}{M}=\frac{x+\sqrt{x}+1}{\sqrt{x}}=\sqrt{x}+\frac{1}{\sqrt{x}}+1\ge2+1=3\)
=> M \(\le\)1/3
=> GTLN của M =1/ 3 khi \(\sqrt{x}=\frac{1}{\sqrt{x}}\Leftrightarrow x=1\) thỏa mãn
Vậy max M = 1/3 tại x = 1