Rút gọn: 1 1 - 2 - 1 2

Khách

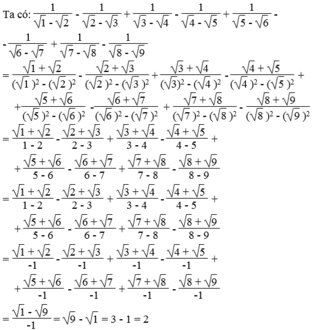
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn lớp

Chọn môn

Mua vip

Pham Trong Bach

5 tháng 8 2018

Rút gọn: 1 1 - 2 - 1 2 - 3 + 1 3 - 4 - 1 4 - 5 + 1 5 - 6 - 1 6 - 7 + 1 7 - 8 - 1 8 - 9

#Toán lớp 9

Cao Minh Tâm

5 tháng 8 2018

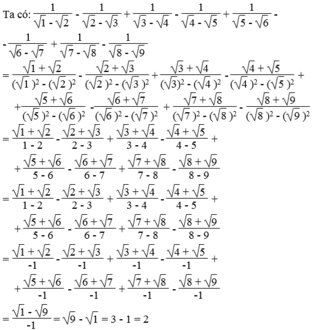
Giải sách bài tập Toán 9 | Giải bài tập Sách bài tập Toán 9

Đúng(0)

Các câu hỏi dưới đây có thể giống với câu hỏi trên

Sách Giáo Khoa

24 tháng 4 2017

Rút gọn :

\(\dfrac{1}{\sqrt{1}-\sqrt{2}}-\dfrac{1}{\sqrt{2}-\sqrt{3}}+\dfrac{1}{\sqrt{3}-\sqrt{4}}-\dfrac{1}{\sqrt{4}-\sqrt{5}}+\dfrac{1}{\sqrt{5}-\sqrt{6}}-\dfrac{1}{\sqrt{6}-\sqrt{7}}+\dfrac{1}{\sqrt{7}-\sqrt{8}}-\dfrac{1}{\sqrt{8}-\sqrt{9}}\)

#Toán lớp 9

ngonhuminh

10 tháng 5 2017

\(A=-\sqrt{2}-\sqrt{1}+\sqrt{2}+\sqrt{3}-\sqrt{3}-\sqrt{4}+....-\sqrt{7}-\sqrt{8}+\sqrt{8}+\sqrt{9}\)

\(A=\sqrt{9}-\sqrt{1}=3-1=2\)

Đúng(0)

hoangkunvai

7 tháng 6 2019 - olm

Rút gọn : \(\frac{1}{\sqrt{1}-\sqrt{2}}-\frac{1}{\sqrt{2}-\sqrt{3}}+\frac{1}{\sqrt{3}-\sqrt{4}}-\frac{1}{\sqrt{4}-\sqrt{5}}+\frac{1}{\sqrt{5}-\sqrt{6}}-\frac{1}{\sqrt{6}-\sqrt{7}}+\frac{1}{\sqrt{7}-\sqrt{8}}-\frac{1}{\sqrt{8}-\sqrt{9}}\)

#Toán lớp 9

Thanh Tùng DZ

7 tháng 6 2019

với n >0, ta có :

\(\left(\sqrt{n+1}+\sqrt{n}\right)\left(\sqrt{n+1}-\sqrt{n}\right)=n+1-n=1\Rightarrow\frac{1}{\sqrt{n+1}-\sqrt{n}}=\sqrt{n+1}+\sqrt{n}\)

Gọi biểu thức đã cho là A

\(A=\frac{1}{-\left(\sqrt{2}-\sqrt{1}\right)}-\frac{1}{-\left(\sqrt{3}-\sqrt{2}\right)}+...+\frac{1}{-\left(\sqrt{8}-\sqrt{7}\right)}-\frac{1}{-\left(\sqrt{9}-\sqrt{8}\right)}\)

\(A=-\frac{1}{\sqrt{2}-\sqrt{1}}+\frac{1}{\sqrt{3}-\sqrt{2}}-...-\frac{1}{\sqrt{8}-\sqrt{7}}+\frac{1}{\sqrt{9}-\sqrt{8}}\)

\(A=-\left(\sqrt{2}+\sqrt{1}\right)+\left(\sqrt{3}+\sqrt{2}\right)-...-\left(\sqrt{8}+\sqrt{7}\right)+\left(\sqrt{9}+\sqrt{8}\right)\)

\(A=-\sqrt{1}+\sqrt{9}=2\)

Đúng(0)

shitbo

7 tháng 6 2019

\(\frac{1}{\sqrt{n}-\sqrt{n+1}}=\frac{\sqrt{n}+\sqrt{n+1}}{\left(\sqrt{n+1}+\sqrt{n}\right)\left(\sqrt{n}-\sqrt{n+1}\right)}=-\sqrt{n}-\sqrt{n+1}\)

Đúng(0)

dinh thi ngoc ha

21 tháng 9 2017 - olm

1+2+3+4+5+6+7+8+9-1-2-3-4-5-6-7-8-9*1*2*3*4*5*6*7*8*9:1:2:3:4:5:6:7:8:9=???

#Toán lớp 9

Ngọc Trân

21 tháng 9 2017

14dm5cm=14,5dm;3dm7cm=3,7dm

chu vi hình chữ nhật đó là:

(14,5+3,7)x2=36,4(dm)

ĐS:36,4dm

Đúng(0)

Chu Quyen Nhan

21 tháng 9 2017

14 dm 5 cm = 14,5 dm

3 dm 7 cm = 3,7 dm

Chiều rộng HCN là :

14,5 - 3,7 = 10,8 ( dm )

chu vi HCN là :

( 14,5 + 10,8 ) x 2 = 50,6 ( dm )

ĐS:..

Đúng(0)

....

24 tháng 6 2021

rút gọn các biểu thức sau:

a \(\sqrt[3]{8\sqrt{5}-16}.\sqrt[3]{8\sqrt{5}+16}\)

b \(\sqrt[3]{7-5\sqrt{2}}-\sqrt[6]{8}\)

c \(\sqrt[3]{4}.\sqrt[3]{1-\sqrt{3}}.\sqrt[6]{4+2\sqrt{3}}\)

d \(\dfrac{2}{\sqrt[3]{3}-1}-\dfrac{4}{\sqrt[3]{9}-\sqrt[3]{3}+1}\)

#Toán lớp 9

Yeutoanhoc

24 tháng 6 2021

`c)root{3}{4}.root{3}{1-sqrt3}.root{6}{(sqrt3+1)^2}`

`=root{3}{4(1-sqrt3)}.root{3}{1+sqrt3}`

`=root{3}{4(1-sqrt3)(1+sqrt3)}`

`=root{3}{4(1-3)}=-2`

`d)2/(root{3}{3}-1)-4/(root{9}-root{3}{3}+1)`

`=(2(root{3}{9}+root{3}{3}+1))/(3-1)-(4(root{3}{3}+1))/(3+1)`

`=root{3}{9}+root{3}{3}+1-root{3}{3}-1`

`=root{3}{9}`

Đúng(3)

Yeutoanhoc

24 tháng 6 2021

`a)root{3}{8sqrt5-16}.root{3}{8sqrt5+16}`

`=root{3}{(8sqrt5-16)(8sqrt5+16)}`

`=root{3}{320-256}`

`=root{3}{64}=4`

`b)root{3}{7-5sqrt2}-root{6}{8}`

`=root{3}{1-3.sqrt{2}+3.2.1-2sqrt2}-root{6}{(2)^3}`

`=root{3}{(1-sqrt2)^3}-sqrt2`

`=1-sqrt2-sqrt2=1-2sqrt2`

Đúng(2)

Lê Thảo Linh

5 tháng 9 2015 - olm

Rút gọn \(\frac{1}{\sqrt{1}-\sqrt{2}}-\frac{1}{\sqrt{2}-\sqrt{3}}+\frac{1}{\sqrt{3}-\sqrt{4}}-\frac{1}{\sqrt{4}-\sqrt{5}}+\frac{1}{\sqrt{5}-\sqrt{6}}+\frac{1}{\sqrt{6}-\sqrt{7}}+\frac{1}{\sqrt{7}-\sqrt{8}}+\frac{1}{\sqrt{8}-\sqrt{9}}\)

#Toán lớp 9

Nguyễn Minh Triết

30 tháng 8 2016

Phân tích mỗi hạng tử theo kiểu như dưới đây

\(\frac{\sqrt{1}+\sqrt{2}}{\left(\sqrt{1}\right)^2-\left(\sqrt{2}\right)^2}\)

\(\frac{\sqrt{2}+\sqrt{3}}{\left(\sqrt{2}\right)^2-\left(\sqrt{3}\right)^2}\)

Khi đó mọi mẫu đều bằng -1

Bạn tiếp tục làm và kết quả nhận được là \(1-\sqrt{9}\)

Đúng(0)

chu tien dat

19 tháng 9 2016 - olm

rút gọn

\(\frac{1}{\sqrt{1}-\sqrt{2}}-\frac{1}{\sqrt{2}-\sqrt{3}}+\frac{1}{\sqrt{3}-\sqrt{4}}-\frac{1}{\sqrt{4}-\sqrt{5}}+\frac{1}{\sqrt{5}-\sqrt{6}}-\frac{1}{\sqrt{6}-\sqrt{7}}+\frac{1}{\sqrt{7}-\sqrt{8}}\)

\(-\frac{1}{\sqrt{8}-\sqrt{9}}\)

#Toán lớp 9

Arceus Official

14 tháng 7 2017 - olm

\(\frac{1}{\sqrt{9}-\sqrt{8}}-\frac{1}{\sqrt{8}-\sqrt{7}}+\frac{1}{\sqrt{7}-\sqrt{6}}-\frac{1}{\sqrt{6}-\sqrt{5}}+\frac{1}{\sqrt{5}-\sqrt{4}}\)rút gọn

#Toán lớp 9

nguyễn văn sơn

22 tháng 6 2016 - olm

1+1+1=6

2+2+2=6

3×3÷3=6

√4+√4+√4=6

5+5÷5=6

6×6÷6=6

7 ? 7 ? 7=6

8 ? 8 ? 8 =6

9 ? 9 ? 9=6

10 ? 10 ? 10=6

#Toán lớp 9

Lemon

5 tháng 12 2019 - olm

Rút gọn bth sau:

a) (√7+√5)/(√7-√5)+(√7-√5)/(√7+√5)

b) (4+√2-√3-√6+√8)/(2+√2-√3)

c) M=(√3+1).√(14-6√3)/(5+√3)

#Toán lớp 9

Laura

5 tháng 12 2019

\(a)\frac{\sqrt{7}+\sqrt{5}}{\sqrt{7}-\sqrt{5}}+\frac{\sqrt{7}-\sqrt{5}}{\sqrt{7}+\sqrt{5}}\)

\(=\frac{\left(\sqrt{7}+\sqrt{5}\right)^2+\left(\sqrt{7}+\sqrt{5}\right)^2}{\left(\sqrt{7}-\sqrt{5}\right)\left(\sqrt{7}+\sqrt{5}\right)}\)

\(=\frac{7+2\sqrt{35}+5+7-2\sqrt{35}+5}{7-5}\)

\(=\frac{24}{2}\)

\(=12\)

\(b)\frac{4+\sqrt{2}-\sqrt{3}-\sqrt{6}+\sqrt{8}}{2+\sqrt{2}-\sqrt{3}}\)

\(=\frac{\left(2+\sqrt{2}-\sqrt{3}\right)+\left(2+\sqrt{8}-\sqrt{6}\right)}{2+\sqrt{2}-\sqrt{3}}\)

\(=\frac{\left(2+\sqrt{2}-\sqrt{3}\right)+\sqrt{2}\left(\sqrt{2}+2-\sqrt{3}\right)}{2+\sqrt{2}-\sqrt{3}}\)

\(=\frac{\left(2+\sqrt{2}-\sqrt{3}\right)\left(1+\sqrt{2}\right)}{2+\sqrt{2}-\sqrt{3}}\)

\(=1+\sqrt{2}\)

\(c)A=\left(\sqrt{3}+1\right)\sqrt{\frac{14-6\sqrt{3}}{5+\sqrt{3}}}\)

\(A=\left(\sqrt{3}+1\right)\sqrt{\frac{\left(14-6\sqrt{3}\right)\left(5-\sqrt{3}\right)}{\left(5+\sqrt{3}\right)\left(5-\sqrt{3}\right)}}\)

\(A=\left(\sqrt{3}+1\right)\sqrt{\frac{70-14\sqrt{3}-30\sqrt{3}+18}{25-3}}\)

\(A=\left(\sqrt{3}+1\right)\sqrt{\frac{88-44\sqrt{3}}{22}}\)

\(A=\left(\sqrt{3}+1\right)\sqrt{\frac{44\left(2-\sqrt{3}\right)}{22}}\)

\(A=\left(\sqrt{3}+1\right)\sqrt{2\left(2-\sqrt{3}\right)}\)

\(A=\left(\sqrt{3}+1\right)\sqrt{4+2\sqrt{3}}\)

\(A=\left(\sqrt{3}+1\right)\sqrt{\left(\sqrt{3}-1\right)^2}\)

\(A=\left(\sqrt{3}+1\right)\left(\sqrt{3}-1\right)\)

\(A=3-1=2\)

P/s: nếu đề là vậy thì t ra kết quả như vậy ạ, nhưng lần sau khi đăng câu hỏi bạn nên viết rõ hơn ra nhé

Đúng(0)

Kaitou Kid

16 tháng 6 2017 - olm

Đề bài: Điền dấu thích hợp để được phép tính đúng:

1 1 1 = 6

2 2 2 = 6

3 3 3 = 6

4 4 4 = 6

5 5 5 = 6

7 7 7 = 6

8 8 8 = 6

9 9 9 = 6

10 10 10 = 6

giúp nhé, giải nhanh nhanh gọn gọn, không rắc rối ? Ok ?

#Toán lớp 9

Lê Hiển Vinh

16 tháng 6 2017

(1+1+1)! = 3! = 6

2+2+2=6

3x3-3=6

\(\sqrt{4}+\sqrt{4}+\sqrt{4}=6\)

5:5+5=6

6+(6-6)=6

7-7:7=6

\(8-\sqrt{\sqrt{8+8}}=6\)

\(\sqrt{9}.\sqrt{9}-\sqrt{9}=6\)

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP