Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

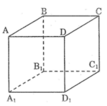
a. Ta có: A1B1 // mp(ABCD)
A1B1 // mp(CDD1C1)
b. Ta có: AC // A1C1
Suy ra: AC không thuộc mp(A1B1C1)

a) Các đường thẳng song song với nhau:
- Hai đường thẳng mép thước kẻ đối diện nhau.
- Hai đường thẳng mép bàn đối diện nhau.
b) Các đường thẳng cắt nhau:
- Các đường thẳng góc tường và chân tường là hai đường thẳng cắt nhau.
- Hai thanh chắn khung cửa sổ cắt nhau.
c) Các mặt phẳng song song với nhau
- Mặt sàn nhà và mặt trần nhà là hai mặt phẳng song song
d) Các đường thẳng vuông góc với nhau
- Hai cạnh góc vuông của thước eke
e) Các đường thẳng vuông góc với các mặt phẳng:
- Đường góc tường vuông góc với mặt sàn hoặc với trần nhà.
f) Các mặt phẳng vuông góc với nhau:
- Tường nhà vuông góc với nền nhà.

\(a^3+b^3=2.\left(c^3-8d^3\right)\)
\(\Leftrightarrow a^3+b^3+c^3+d^3=3c^2-15d^3⋮3\)
\(a^3+b^3+c^3+d^3-\left(a+b+c+d\right)⋮3\Rightarrow a+b+c+d⋮3\)
tự c/n \(a^3+b^3+c^3+d^3-\left(a+b+c+d\right)⋮3\)nha, gợi ý 1 cái rồi còn lại tương tự
\(a^3-a=a.\left(a^2-1\right)=a.\left(a-1\right).\left(a+1\right)\)chia hết cho 3( vì a,b,c,d thuộc Z)
ợ mk ngu toán lắm, bn lm ơn giải rõ ràng ra hộ nhaaa

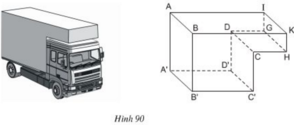
a) Những đường thẳng song song với mặt phẳng (ABKI) là A’B’; D’C’; DC; GH.
b) Những đường thẳng vuông góc với mặt phẳng (DCC'D') là A'D'; B'C'; DG; CH; AI; BK.
c) Ta có: A'D' ⊥ (CDD'C') mà A’D’ nằm trong mặt phẳng (A’D’C’B’) nên (A'B'C'D') ⊥ (CDD'C')

Ta có DE//AC \(\Rightarrow\dfrac{AE}{AB}=\dfrac{CD}{BC}\) (Talet)
Ta có DF//AB \(\Rightarrow\dfrac{AF}{AC}=\dfrac{BD}{BC}\) (Talet)
\(\Rightarrow\dfrac{AE}{AB}+\dfrac{AF}{AC}=\dfrac{CD}{BC}+\dfrac{BD}{BC}=\dfrac{BC}{BC}=1\left(dpcm\right)\)

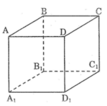

Ta có:AC // A 1 C 1
Suy ra: AC không thuộc mp( A 1 B 1 C 1 )