Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a,b,c làm như bạn trên nhé. Tuy nhiên câu d, cách của bạn đó làm dài và k hay, mình làm cách khác:
Mình mượn tạm hình vẽ của bạn đó luôn :))))
Gọi I là trung điểm của AB. vì dây AB cố định (gt) => I cố định
=> \(OI\perp AB\)(Quan hệ vuông góc giữa đường kính và dây cung) => \(\widehat{OIA}=90^o\)(1)
Do \(AM\perp CD\)tại M (gt) => \(\widehat{OMA}=90^o\)(2)
Từ (1) và (2) => Tứ giác OMIA là tứ giác nội tiếp (DHNB) => \(\widehat{IMN}=\widehat{OAI}=\widehat{OAB}\)(cùng bù với \(\widehat{OMI}\)) (3)
Lại có: \(\widehat{OIB}=\widehat{ONB}=90^o\)=> tứ giác OINB là tứ giác nội tiếp(DHNB) => \(\widehat{INO}=\widehat{INM}=\widehat{OBI}\)(Cùng chắn \(\widebat{OI}\)) = \(\widehat{OBA}\)(4)
\(\Delta OAB\)Cân tại O do OA=OB=R => \(\widehat{OAB}=\widehat{OBA}\)(t/c) (5)
Từ (3),(4) và (5) => \(\widehat{INM}=\widehat{IMN}\Rightarrow\Delta IMN\)cân tại I (DHNB) => IM =IN (đ/n) (6)
Do CMHA nội tiếp (cmt) => \(\widehat{IHM}=\widehat{ACM}=\widehat{ACO}\)(Cùng bù với \(\widehat{AHM}\)) (7)
Ta có: \(\widehat{IMH}=\widehat{NMH}-\widehat{IMN}\)mà \(\widehat{NMH}=\widehat{CAH}=\widehat{CAB}\)(Cùng bù \(\widehat{CMH}\))
\(\widehat{IMN}=\widehat{INM}=\widehat{INO}=\widehat{IBO}=\widehat{ABO}=\widehat{OAB}\)(CMT) => \(\widehat{IMH}=\widehat{CAB}-\widehat{OAB}=\widehat{CAO}\)(8)
Mặt khác \(\Delta OAC\)Cân tại O do OA=OC=R => \(\widehat{CAO}=\widehat{ACO}\)(9)
Từ (7),(8) và (9) => \(\widehat{IHM}=\widehat{IMH}\Rightarrow\Delta IMH\)cân tại I (DHNB) => IM = IH (đ/n) (10)
Từ (6) và (10) => IM = IH = IN => I là tâm đường tròn ngoại tiếp \(\Delta HMN\)(I cố định) => Đpcm
A B C O D H M N L R G I
a) Xét tứ giác CMHA có: ^CMA=^CHA=900 => Tứ giác CMHA nội tiếp đường tròn
Dựa theo tính chất đừng trung tuyến trong tam giác vuông, ta tìm được tâm G của đường tròn ngoại tiếp tứ giác CMHA là trung điểm của AC.
b) Do tứ giác CMHA nội tiếp (G) => ^ACM+^AHM=1800. Mà ^AHM+^MHB=1800
=> ^ACM=^MHB hay ^ACD=^MHB (1)
Ta thấy tứ giác ACBD nội tiếp (O) => ^ACD=^ABD (2)
Từ (1) và (2) => ^MHB=^ABD. Mà 2 góc này nằm ở vị trí so le trg nên HM // BD (3)
Ta có: Đương tròn (O) có đường kính CD, B thuộc cung CD => ^CBD=900
=> BD vuông góc với BC (4)
Từ (3) và (4) => HM vuông góc với BC (đpcm).
c) Ta có tứ giác CMHA nội tiếp (G) => ^CAH+^CMH=1800. Mà ^CMH+^HMN=1800
=> ^CAH=^HMN hay ^CAB=^HMN
Chứng minh tương tự phần a ta được tứ giác CHNB nội tiếp đường tròn
Từ đó suy ra ^CNH=^CBH hay ^MNH=^CBA
Xét \(\Delta\)HMN và \(\Delta\)CAB: ^CAB=^HMN; ^MNH=^CBA (cmt)
=> \(\Delta\)HMN ~ \(\Delta\)CAB (g.g) (đpcm).
d) Gọi giao điểm của đường tròn ngoại tiếp tâm I \(\Delta\)HMN với AM và AB lần lượt là R và L
Dễ thấy tứ giác HRMN nội tiếp (I) => ^HNM+^HRM=1800. Mà ^ARH+^HRM=1800
=> ^HNM=^ARH hay ^CNH=^ARH (^HNM=^CNH)
Tứ giác CMHA nội tiếp (G) => ^MAH=^MCH hay ^RAH=^NCH
Xét \(\Delta\)AHR và \(\Delta\)CHN: ^CNH=^ARH; ^NCH=^RAH => \(\Delta\)AHR ~ \(\Delta\)CHN (g.g)
=> \(\frac{AH}{CH}=\frac{HR}{HN}\)(5)
Dễ thấy: ^AHR=^CHN => ^AHC+^CHR=^CHR+^RHN => ^AHC=^RHN
Mà ^AHC=900 => ^RHN=900
Tứ giác CHNB nội tiếp đường tròn => ^HBN=^HCN hay ^LBN=^HCN
Lại có: Tứ giác HMLN nội tiếp I => ^HLN=^HMN => 1800-^HLN=1800-^HMN
=> ^NLB=^HMC
Theo t/c góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung => HMC=^NHC=> ^NLB=^NHC
Xét \(\Delta\)CHN và \(\Delta\)BLN: ^HCN=^LBN; ^NHC=^NLB (cmt) => \(\Delta\)CHN ~ \(\Delta\)BLN (g.g)
=> \(\frac{BL}{CH}=\frac{LN}{HN}\)(6)
Xét (I) có đường kính HL; R thuộc cung HL => ^HRL=900 . Tương tự ta có: ^HNL=900
Xét tứ giác HRLN: ^HRL=^HNL=^RHN=900 (cmt) => Tứ giác HRLN là hình chữ nhật
=> HR=LN (2 cạnh đối) (7)
Từ (5); (6) và (7) => \(\frac{AH}{CH}=\frac{BL}{CH}\)=> \(AH=BL\)
I là trung điểm HL => IH=IL => IH+AH=IL+BL => AI=BI => I là trung điểm của AB
Do dây cung AB cố định => Trung điểm I của AB là điểm cố định.
Mà I là tâm đường tròn ngoại tiếp \(\Delta\)HMN
Suy ra tâm đường tròn ngoại tiếp \(\Delta\)HMN là điểm cố định khi C di động trên cung lớn AB (đpcm).

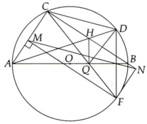
a, Tứ giác BDQH nội tiếp vì B D H ^ + B Q H ^ = 180 0
b, Vì tứ giác ACHQ nội tiếp =>
C
A
H
^
=
C
Q
H
^
Vì tứ giác ACDF nội tiếp => C A D ^ = C F D ^
Từ đó có C Q H ^ = C F D ^ mà 2 góc ở vị trí đồng vị => DF//HQ
c, Ta có H Q D ^ = H B D ^ (câu a)
H B D ^ = C A D ^ = 1 2 s đ C D ⏜
C A D ^ = C Q H ^ (ACHQ cũng nội tiếp)
=>
H
Q
D
^
=
H
Q
C
^
=> QH là phân giác
C
Q
D
^
Mặt khác chứng minh được CH là phân giác góc Q C D ^
Trong tam giác QCD có H là giao của ba đường phân giác nên H là tâm đường tròn nội tiếp => H cách đều 3 cạnh CD, CQ, DQ
d, Vì CMFN là hình chữ nhật nên MN và CF cắt nhau tại trung điểm của mỗi đường.
Trong tam giác FCD có MN//CD và MN đi qua trung điểm CF nên MN đi qua trung điểm DF
Mặt khác AB đi qua trung điểm của DF nên 3 đường thẳng MN, AB, DF đồng quy
bạn giải thích lại giúp mình câu b được không ạ? tại mình không hiểu câu đó lắm, mình cảm ơn!