Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:
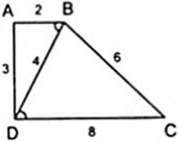
BA/BD = AD/BC = BD/CD = 1/2 ⇒ Δ BAD ∼ Δ DBC ( c - c - c )

Ta có:
BA/BD = AD/BC = BD/CD = 1/2 ⇒ Δ BAD ∼ Δ DBC ( c - c - c )


Bài 3: Xét tam giác BCD có :
BC=DC ( gt )
-> tam giác BCD cân tại C
-> ^B1 = ^D1 ( 2 góc đáy )(1)
Mặt khác : BD là tia phân giác của ^D
-> ^D1 =^D2 (2)
Từ (1) và (2) suy ra : ^B1 = ^D2 ( cùng = ^D1 )
-> BC // DA ( có cặp góc so le trong = nhau )
-> Tứ giác ABCD là hình thang ( có 2 cạnh đối song song )
Bài 4 : Từ B hạ BH vuông góc với DC (1)
Do tứ giác ABCD có ^A=^D = 900 ( gt)(2)
Từ (1) và (2) suy ra : Tứ giác ABCD là HCN ( dấu hiệu nhận biết )
-> DH = AB =2 cm ( 2 cạnh đối )
BH = AD= 2 cm ( 2 cạnh đối)
Mà DH +HC = DC= 4 (cm) ( gt)
-> HC = 2 ( cm)
Áp dụng định lí Py ta go trong tam giác vuông BHC có :
BH2 + HC2 = BC2
-> 22 + 22 = BC2
Vậy BC = \(\sqrt{8}\)(cm)
hình vẽ chỉ minh họa thôi bạn mà vẽ thì vẽ số liệu chính xác hơn nha !
Ở bài 4 có thể chứng minh tứ giác đó là hình vuông nhá bạn

Câu 1:
Gọi mỗi đinh của tứ giác là A, B, C, D. Các góc ngoài tương ứng lần lượt là A1, B1, C1, D1
Ta có: A+ B+ C+ D+ A1+ B1+ C1+ D1= 720 độ
Ma A+ B+ C+ D= 360 độ nên A1+ B1+ C1+ D1= 720 - 360= 360 độ
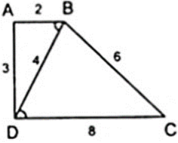
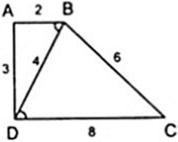
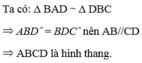
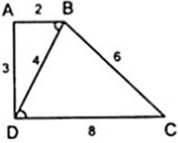
Ta có: Δ BAD ∼ Δ DBC
⇒ A B D ^ = B D C ^ nên AB//CD
⇒ ABCD là hình thang.