Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

bài này dễ mà bạn
có MTA=1/2 sd AT
ABT=1/2 sd AT
\(\Rightarrow\)MTA=MTB
xét tam giác MTA và MBT
M chung
MTA=MTB
tam giác MTA dong dang MBT
\(\Rightarrow\)MT/AB=MA/MT\(\Rightarrow\)MT2=MA.MT

Xét ΔOTM vuông tại T có \(OM^2=OT^2+TM^2\)
=>\(TM^2=OM^2-OT^2\)
=>\(MT^2=d^2-R^2\left(1\right)\)
Xét (O) có
\(\widehat{MTA}\) là góc tạo bởi tiếp tuyến TM và dây cung TA
\(\widehat{TBA}\) là góc nội tiếp chắn cung TA
Do đó: \(\widehat{MTA}=\widehat{TBA}\)
=>\(\widehat{MTA}=\widehat{MBT}\)
Xét ΔMTA và ΔMBT có
\(\widehat{MTA}=\widehat{MBT}\)
\(\widehat{TMA}\) chung
Do đó: ΔMTA đồng dạng với ΔMBT
=>\(\dfrac{MT}{MB}=\dfrac{MA}{MT}\)
=>\(MT^2=MA\cdot MB\left(2\right)\)
Từ (1) và (2) suy ra \(MA\cdot MB=MT^2=d^2-R^2\)
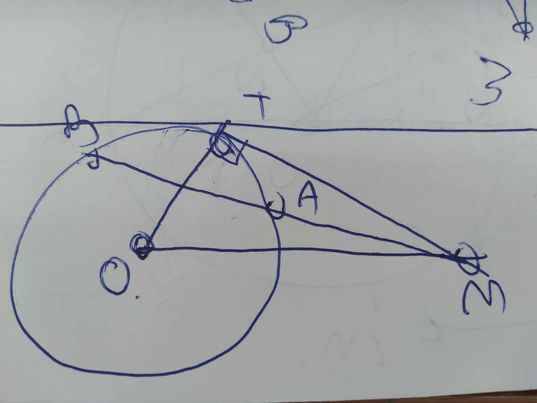

Xét ΔOTM vuông tại T có \(OM^2=OT^2+TM^2\)
=>\(TM^2=OM^2-OT^2\)
=>\(MT^2=d^2-R^2\left(1\right)\)
Xét (O) có
\(\widehat{MTA}\) là góc tạo bởi tiếp tuyến TM và dây cung TA
\(\widehat{TBA}\) là góc nội tiếp chắn cung TA
Do đó: \(\widehat{MTA}=\widehat{TBA}\)
=>\(\widehat{MTA}=\widehat{MBT}\)
Xét ΔMTA và ΔMBT có
\(\widehat{MTA}=\widehat{MBT}\)
\(\widehat{TMA}\) chung
Do đó: ΔMTA đồng dạng với ΔMBT
=>\(\dfrac{MT}{MB}=\dfrac{MA}{MT}\)
=>\(MT^2=MA\cdot MB\left(2\right)\)
Từ (1) và (2) suy ra \(MA\cdot MB=MT^2=d^2-R^2\)
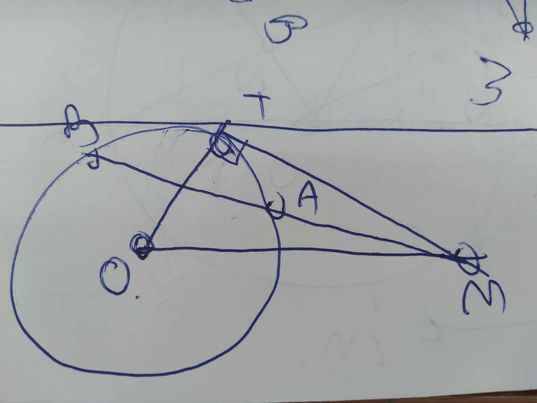

a) Ta có: \(\widehat{ATM}=\frac{1}{2}Sđ\widebat{AT}\),
\(\widehat{ABT}=\frac{1}{2}Sđ\widebat{AT}\).
=> \(\widehat{ATM}=\widehat{ABT}\).
b) \(\Delta MAT\)và \(\Delta MTB\)có góc M chung, góc MTA = góc MBT ( theo câu a).
Do đó \(\Delta MAT\)đồng dạng với \(\Delta MTB\)(g-g), ta có:
\(\frac{MA}{MT}=\frac{MT}{MB}\)=> MT2 = MA.MB.
T M A O B
B, Xét tam giác
MAT và MTB có:
tam giác MTA=\(\widehat{MBT}\)
⇒△MAT∼△MTB(g.g)
⇒MAMT=MTMB⇔MT2=MA.MB (đpcm)

M T A B O
xét (o) có ^MTA là góc tạo bởi tt à dc chắn cung TA
^TBM là góc nt chắn cung TA
=> ^MTA = ^TBM (hq)
xét tg MTA và tg MBT có ^M chung
=> tg MTA đồng dạng tg MBT (g-g)
=> MT/MB = MA/MT
=> MT^2 = MB.MA
bài 2 tự kẻ hình đi
a, như bài 1
b, tg MAC đồng dạng tg MCB (câu a)
=> MA/MC = MC/MB
=> MC^2 = MA.MB (1)
xét tg MCO có ^MCO = 90 do MC là tt
CH _|_ MO
=> mc^2 = mh.mo (ĐL) (2)
(1)(2) => MH.MO = MA.MB
c, xét tg AHC và tg ACB có : ^ACB = ^AHC = 90(do C thuộc đường tròn đk AB)
^cah CHUNG
=> tg AHC đồng dạng tg ACB
=> ^ACH = ^CBA mà ^CBA = ^MCA (Câu a)
=> ^ACH = ^MCA
=> CA là pg...
làm gì có tam giác MAB bạn
- Đề bài sai rồi bạn.