Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có tọa độ vectơ \(\overrightarrow {OB} ,\overrightarrow {OA} \) chính là tọa độ điểm B và A
Nên ta có \(\overrightarrow {OB} = \left( {{x_B};{y_B}} \right),\overrightarrow {OA} = \left( {{x_A};{y_A}} \right)\)
\(\overrightarrow {AB} = \overrightarrow {OB} - \overrightarrow {OA} = \left( {{x_B};{y_B}} \right) - \left( {{x_A};{y_A}} \right) = ({x_B} - {x_A};{y_B} - {y_A})\)

a) M là trung điểm của đoạn thẳng AB, áp dụng tính chất trung điểm ta có:
\(\overrightarrow {OM} = \frac{1}{2}\left( {\overrightarrow {OA} + \overrightarrow {OB} } \right)\)
b) G là trọng tâm của tam giác ABC, áp dụng tính chất trọng tâm của tam giác ta có:
\(\overrightarrow {OG} = \frac{1}{3}\left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} } \right)\)
c) Ta có \(\overrightarrow {OA} = \left( {{x_A};{y_A}} \right),\overrightarrow {OB} = \left( {{x_B};{y_B}} \right),\overrightarrow {OC} = \left( {{x_C};{y_C}} \right)\)
Suy ra:
\(\begin{array}{l}\overrightarrow {OM} = \frac{1}{2}\left( {\overrightarrow {OA} + \overrightarrow {OB} } \right) = \frac{1}{2}\left[ {\left( {{x_A};{y_A}} \right) + \left( {{x_B};{y_B}} \right)} \right]\\ = \left( {\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2}} \right)\end{array}\)
\(\begin{array}{l}
\overrightarrow {OG} = \frac{1}{3}\left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} } \right) = \frac{1}{3}\left[ {\left( {{x_A};{y_A}} \right) + \left( {{x_B};{y_B}} \right) + \left( {{x_c};{y_c}} \right)} \right]\\
= \left( {\frac{{{x_A} + {x_B} + {x_C}}}{3};\frac{{{y_A} + {y_B} + {y_C}}}{3}} \right)
\end{array}\)
Mà ta có tọa độ vectơ \(\overrightarrow {OM} \) chính là tọa độ điểm M, nên ta có
Tọa độ điểm M là \(\left( {{x_M};{y_M}} \right) = \left( {\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2}} \right)\)
Tọa độ điểm G là \(\left( {\frac{{{x_A} + {x_B} + {x_C}}}{3};\frac{{{y_A} + {y_B} + {y_C}}}{3}} \right)\)

a) Ta có vectơ \(\overrightarrow {OM} \) biểu diễn theo hai vectơ \(\overrightarrow {OA} \) và \(\overrightarrow {OB} \) là: \(\overrightarrow {OM} = \frac{1}{2}\left( {\overrightarrow {OA} + \overrightarrow {OB} } \right)\)
b) Do tọa độ hai điểm A và B là: \(A\left( {{x_A},{y_A}} \right),B\left( {{x_B},{y_B}} \right)\) nên ta có:\(\overrightarrow {OA} = \left( {{x_A},{y_A}} \right),\overrightarrow {OB} = \left( {{x_B},{y_B}} \right)\)
Vậy \(\overrightarrow {OM} = \frac{1}{2}\left( {\overrightarrow {OA} + \overrightarrow {OB} } \right) = \frac{1}{2}\left( {{x_A} + {x_B};{y_A} + {y_B}} \right) = \left( {\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2}} \right)\)
Tọa độ điểm M chính là tọa độ của vectơ nên tọa độ M là \(M\left( {\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2}} \right)\)

a) \(\overrightarrow a \bot \overrightarrow b \Leftrightarrow \overrightarrow a .\overrightarrow b = \overrightarrow 0 \Leftrightarrow {a_1}{b_1} + {a_2}{b_2} = 0\)
b) \(\overrightarrow a \) và \(\overrightarrow b \) cùng phương \( \Leftrightarrow \left\{ \begin{array}{l}{a_1} = t{b_1}\\{a_2} = t{b_2}\end{array} \right.\) hay \(\left\{ \begin{array}{l}{b_1} = k{a_1}\\{b_2} = k{a_2}\end{array} \right.\)
\( \Leftrightarrow {a_1}{b_2} - {a_2}{b_1} = {a_1}.k{a_2} - {a_2}.k{a_1} = 0\)
c) \(\left| {\overrightarrow a } \right| = \sqrt {{{\left( {\overrightarrow a } \right)}^2}} = \sqrt {{a_1}^2 + {a_2}^2} \)
d) \(\overrightarrow {AB} = ({x_B} - {x_A};{y_B} - {y_A}) \Rightarrow AB = \sqrt {{{\left( {\overrightarrow {AB} } \right)}^2}} \)
\( = \sqrt {{{\left( {{x_B} - {x_A}} \right)}^2} + {{\left( {{y_B} - {y_A}} \right)}^2}} \)
e) \(\cos (\overrightarrow a ,\overrightarrow b ) = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}} = \frac{{{a_1}{b_1} + {a_2}{b_2}}}{{\sqrt {{a_1}^2 + {a_2}^2} .\sqrt {{b_1}^2 + {b_2}^2} }}\)

Phương trình hoành độ giao điểm là:
\(x^2-6x=-x^2-4\)
=>\(x^2-6x+x^2+4=0\)
=>\(2x^2-6x+4=0\)
=>\(x^2-3x+2=0\)
=>(x-1)(x-2)=0
=>\(\left[{}\begin{matrix}x-1=0\\x-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\)
Khi x=1 thì \(y=-1^2-4=-1-4=-5\)
Khi x=2 thì \(y=-2^2-4=-8\)
Vậy: A(1;-5); B(2;-8)
\(y_A+y_B=\left(-5\right)+\left(-8\right)=-13\)

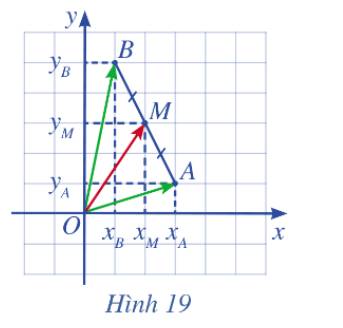
a) Dựa vào hình vẽ, ta có: \({x_A} = 2,{y_A} = 2\) và \({x_B} = 4,{y_B} = 3\)
b) Để \(\overrightarrow {OM} {\rm{ }} = {\rm{ }}\overrightarrow {AB} \) thì điểm M phải có tọa độ: \(M\left( {1;2} \right)\). Do đó, toạn độ của vectơ\(\overrightarrow {AB} \)là \(\overrightarrow {AB} = \left( {2;1} \right)\)
c) Do \(\overrightarrow {AB} = \left( {2;1} \right)\) nên \(a = 2,b = 1\)
Ta có: \({x_B} - {x_A} = 4 - 2 = 2\), \({y_B} - {y_A} = 3 - 2 = 1\)
Vậy \({x_B} - {x_A} = a\) và \({y_B} - {y_A} = b\)

Phương trình hoành độ giao điểm:
\(x^2=2x+3-m^2\Leftrightarrow x^2-2x+m^2-3=0\)
Để 2 đồ thị cắt nhau tại 2 điểm pb
\(\Leftrightarrow\Delta'>0\Leftrightarrow4-m^2>0\Rightarrow-2< m< 2\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_A+x_B=2\\x_Ax_B=m^2-3\end{matrix}\right.\)
\(\Rightarrow T=\left|m^2-3-4-2\right|=\left|m^2-9\right|\)
Do \(0\le m^2< 4\Rightarrow-9\le m^2-9< -5\)
\(\Rightarrow0< \left|m^2-9\right|\le9\Rightarrow0< T\le9\)
\(\Rightarrow T_{max}=9\) khi \(m=0\)
\(A\left(x_a;y_a\right)\Rightarrow\overrightarrow{IA}=x_a\overrightarrow{i}+y_a\overrightarrow{j}\)
\(B\left(x_b;y_b\right)\Rightarrow\overrightarrow{IB}=x_b\overrightarrow{i}+y_b\overrightarrow{j}\)(Với \(\overrightarrow{i};\overrightarrow{j}\)là hai vector đơn vị của trục Ox,Oy)
\(\Rightarrow\overrightarrow{AB}=\overrightarrow{IB}-\overrightarrow{IA}=\left(x_b-x_a\right)\overrightarrow{i}+\left(y_b-y_a\right)\overrightarrow{j}\)
Vậy tọa độ của vector AB là \(\overrightarrow{AB}=\left(x_b-x_a;y_b-y_a\right).\)