Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(A\left(x_a;y_a\right)\Rightarrow\overrightarrow{IA}=x_a\overrightarrow{i}+y_a\overrightarrow{j}\)
\(B\left(x_b;y_b\right)\Rightarrow\overrightarrow{IB}=x_b\overrightarrow{i}+y_b\overrightarrow{j}\)(Với \(\overrightarrow{i};\overrightarrow{j}\)là hai vector đơn vị của trục Ox,Oy)
\(\Rightarrow\overrightarrow{AB}=\overrightarrow{IB}-\overrightarrow{IA}=\left(x_b-x_a\right)\overrightarrow{i}+\left(y_b-y_a\right)\overrightarrow{j}\)
Vậy tọa độ của vector AB là \(\overrightarrow{AB}=\left(x_b-x_a;y_b-y_a\right).\)

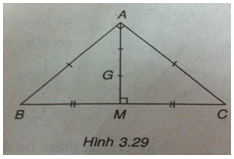
a) M là trung điểm của đoạn thẳng AB, áp dụng tính chất trung điểm ta có:
\(\overrightarrow {OM} = \frac{1}{2}\left( {\overrightarrow {OA} + \overrightarrow {OB} } \right)\)
b) G là trọng tâm của tam giác ABC, áp dụng tính chất trọng tâm của tam giác ta có:
\(\overrightarrow {OG} = \frac{1}{3}\left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} } \right)\)
c) Ta có \(\overrightarrow {OA} = \left( {{x_A};{y_A}} \right),\overrightarrow {OB} = \left( {{x_B};{y_B}} \right),\overrightarrow {OC} = \left( {{x_C};{y_C}} \right)\)
Suy ra:
\(\begin{array}{l}\overrightarrow {OM} = \frac{1}{2}\left( {\overrightarrow {OA} + \overrightarrow {OB} } \right) = \frac{1}{2}\left[ {\left( {{x_A};{y_A}} \right) + \left( {{x_B};{y_B}} \right)} \right]\\ = \left( {\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2}} \right)\end{array}\)
\(\begin{array}{l}
\overrightarrow {OG} = \frac{1}{3}\left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} } \right) = \frac{1}{3}\left[ {\left( {{x_A};{y_A}} \right) + \left( {{x_B};{y_B}} \right) + \left( {{x_c};{y_c}} \right)} \right]\\
= \left( {\frac{{{x_A} + {x_B} + {x_C}}}{3};\frac{{{y_A} + {y_B} + {y_C}}}{3}} \right)
\end{array}\)
Mà ta có tọa độ vectơ \(\overrightarrow {OM} \) chính là tọa độ điểm M, nên ta có
Tọa độ điểm M là \(\left( {{x_M};{y_M}} \right) = \left( {\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2}} \right)\)
Tọa độ điểm G là \(\left( {\frac{{{x_A} + {x_B} + {x_C}}}{3};\frac{{{y_A} + {y_B} + {y_C}}}{3}} \right)\)

Phương trình hoành độ giao điểm:
\(x^2=2x+3-m^2\Leftrightarrow x^2-2x+m^2-3=0\)
Để 2 đồ thị cắt nhau tại 2 điểm pb
\(\Leftrightarrow\Delta'>0\Leftrightarrow4-m^2>0\Rightarrow-2< m< 2\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_A+x_B=2\\x_Ax_B=m^2-3\end{matrix}\right.\)
\(\Rightarrow T=\left|m^2-3-4-2\right|=\left|m^2-9\right|\)
Do \(0\le m^2< 4\Rightarrow-9\le m^2-9< -5\)
\(\Rightarrow0< \left|m^2-9\right|\le9\Rightarrow0< T\le9\)
\(\Rightarrow T_{max}=9\) khi \(m=0\)

bài toán này nghĩ mãi không ra, mình làm theo cách dời hình của lớp 11 nên không thấy hợp lý lắm.
bản thân \(x_B,x_A\)khá lẻ. Để tí nữa mình sửa lại cho chẵn để dẽ tính hơn.